题目内容
5.等差数列{an}的公差d∈(-1,0),$\frac{si{n}^{2}{a}_{3}-co{s}^{2}{a}_{3}+co{s}^{2}{a}_{3}co{s}^{2}{a}_{6}-si{n}^{2}{a}_{3}si{n}^{2}{a}_{6}}{sin({a}_{2}+{a}_{7})}$=1,且a1=$\frac{4π}{5}$,则使得数列{an}的前n项和Sn>0的n的最大值为( )| A. | 11 | B. | 10 | C. | 9 | D. | 8 |
分析 运用二倍角公式和两角和差的余弦公式以及积化和差、和差化积公式的运用,结合等差数列的通项,可得sin3d=-1,3d=-$\frac{π}{2}$,即为d=-$\frac{π}{6}$,运用等差数列的求和公式,结合二次不等式的解法,化简计算即可得到n的最大值.
解答 解:由$\frac{si{n}^{2}{a}_{3}-co{s}^{2}{a}_{3}+co{s}^{2}{a}_{3}co{s}^{2}{a}_{6}-si{n}^{2}{a}_{3}si{n}^{2}{a}_{6}}{sin({a}_{2}+{a}_{7})}$=1,
可得-cos2a3+(cosa3cosa6+sina3sina6)(cosa3cosa6-sina3sina6)=sin(a2+a7),
即为cos(a3-a6)cos(a3+a6)-cos2a3=sin(a3+a6),
$\frac{1}{2}$cos2a3+$\frac{1}{2}$cos2a6-cos2a3=sin(a3+a6),
$\frac{1}{2}$(cos2a6-cos2a3)=sin(a3+a6),
即有-sin(a3+a6)sin(a6-a3)=sin(a3+a6),
由公差d∈(-1,0),且a1=$\frac{4π}{5}$,
则sin(a6-a3)=-1,
即有sin3d=-1,
3d=-$\frac{π}{2}$,即为d=-$\frac{π}{6}$,
则数列{an}的前n项和Sn=$\frac{4π}{5}$•n-$\frac{1}{2}$n(n-1)•$\frac{π}{6}$,
由Sn>0可得0<n<$\frac{53}{5}$,
即有n的最大值为10.
故选B.
点评 本题考查等差数列的通项和求和公式的运用,同时考查三角函数的恒等变换公式的运用,以及二次不等式的解法,属于中档题.

| A. | 与x轴相切的抛物线 | B. | 与x轴相交的抛物线 | ||
| C. | 一条水平直线 | D. | 一条不是水平的直线 |
| A. | {x|x≥0} | B. | {x|x≤1} | C. | {-1,0,1} | D. | R |
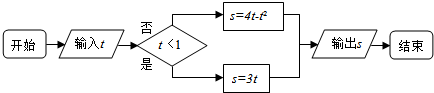
| A. | [-4,3] | B. | [-5,2] | C. | [-3,4] | D. | [-2,5]. |
