题目内容
4.设函数y=2-x-|lgx|的两个零点为x1,x2,则下列结果正确的是( )| A. | x1x2>1 | B. | x1x2=1 | C. | 0<x1x2<1 | D. | x1x2<0 |
分析 此题关键在于画出方程左右两边函数的图象,特别要注意y=|lgx|与y=2-x的单调性,结合图象易知答案.
解答 解:画出函数y=2-x和y=|lgx|的图象,如图示: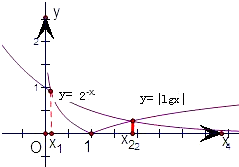
结合图象易知这两个函数的图象有2交点.
交点的横坐标即为方程 2-x=|lgx|的两个根为x1,x2,
结合图形可得:0<x1<1,x2>1,
根据 y=2-x 是减函数,可得 2-x1<2-x2,即|lgx1|>|lgx2|,
∴-lgx1>lgx2,
∴$\frac{1}{{x}_{1}}$>x2,
∴0<x1x2<1,
故选:C.
点评 本题主要考查了函数与方程的综合运用,以及数形结合的思想,属于基础题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
13.sin(-120°)的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $-\frac{1}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |