题目内容

2．已知空间两点P1（-1，3，5），P2（2，4，-3），则|P1P2|等于（　　）
A．$\sqrt{74}$B．3$\sqrt{10}$C．$\sqrt{14}$D．$\sqrt{53}$

分析 直接利用空间距离公式求解即可．

解答 解：空间两点P1（-1，3，5），P2（2，4，-3），
则|P1P2|=$\sqrt{{（2+1）}^{2}+{（4-3）}^{2}+{（-3-5）}^{2}}$=$\sqrt{74}$．
故选：A．

点评 本题考查空间距离公式的应用，考查计算能力．

练习册系列答案
相关题目
12．已知数列{an}的首项a1=2，且an+1=3an-t（n-1）（t∈R），若数列{bn}前n项和为Tn=-n2，且an+1+bn+1=3（an+bn）对任意的n∈N*恒成立．
（1）求t的值；
（2）设数列{anbn+bn2}的前n项和为Sn，问是否存在互不相等且大于2的正整数m，k，r，使得m，k，r成等差数列的同时Sm+1，Sk+1，Sr+1成等比数列？若存在，求出m，k，r的值；若不存在，说明理由．
13．已知tan（2π-θ）=-$\frac{1}{2}$，且θ是第三象限角．
（1）求tanθ的值；
（2）设函数f（x）=$\frac{sin（π+x）-3cos（π+x）+sin（\frac{3}{2}π-x）}{cos（x-\frac{π}{2}）+cos（3π-x）}$，求f（θ）的值．
10．二项式${（{2\sqrt{x}+\frac{1}{{\root{4}{x}}}}）^n}$（n∈N）的展开式中，前三项的系数依次成等差数列，则此展开式有理项的项数是3．
17．运行如下程序框图，如果输入的t∈[-1，3]，则输出s属于（　　）
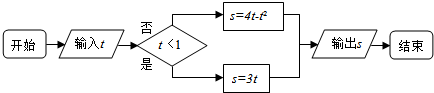
A．[-4，3]B．[-5，2]C．[-3，4]D．[-2，5]．
7．若f（$\frac{1-x}{1+x}$）=$\frac{1-{x}^{2}}{1+{x}^{2}}$，求f（x）．
14．在平面直角坐标系xoy中，已知经过原点O的直线l与圆C：x2+y2-4x-1=0交于A，B两点．
（1）若直线m：ax-2y+a+2=0（a＞0）与圆C相切，切点为B，求直线l的方程；
（2）若OB=2OA，求直线l的方程；
（3）若圆C与x轴的正半轴的交点为D，求△ABD面积的最大值．
12．已知向量$\overrightarrow{m}$=（2cos2x，$\sqrt{3}$），$\overrightarrow{n}$=（1，sin2x），函数f（x）=$\overrightarrow{m}$•$\overrightarrow{n}$-1．
（Ⅰ）求函数f（x）的最小正周期；
（Ⅱ）在△ABC中，a，b，c分别是角A，B，C的对边，且f（C）=2，c=1，ab=2$\sqrt{3}$，且a＞b，求a，b的值．
13．sin（-120°）的值为（　　）
A．$\frac{1}{2}$B．$\frac{{\sqrt{3}}}{2}$C．$-\frac{1}{2}$D．$-\frac{{\sqrt{3}}}{2}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网