题目内容
【题目】已知f(x)为二次函数,且f(x+1)+f(x﹣1)=2x2﹣4x,
(1)求f(x)的解析式;
(2)设g(x)=f(2x)﹣m2x+1,其中x∈[0,1],m为常数且m∈R,求函数g(x)的最小值.
【答案】(1)f(x)=x2﹣2x﹣1(2)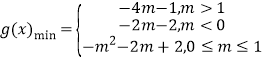
【解析】
(1)因为函数f(x)为二次函数,所以可设函数的解析式为f(x)=ax2+bx+c,且![]() ,利用条件求系数即可;(2)根据(1)所求的二次函数的解析式可写出函数g(x)=f(2x)﹣m2x+1的解析式,整理可得,
,利用条件求系数即可;(2)根据(1)所求的二次函数的解析式可写出函数g(x)=f(2x)﹣m2x+1的解析式,整理可得,![]() ,令t=2x,可构造关于t的二次函数,进而可求其最小值。
,令t=2x,可构造关于t的二次函数,进而可求其最小值。
解:(1)设f(x)=ax2+bx+c,且![]() 。
。
因为f(x+1)+f(x﹣1)=2x2﹣4x,
所以a(x+1)2+b(x+1)+c+a(x﹣1)2+b(x﹣1)+c=2x2﹣4x,所以2ax2+2bx+2a+2c=2x2﹣4x
故有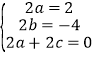 ,即a=1,b=﹣2,c=﹣1,所以f(x)=x2﹣2x﹣1;
,即a=1,b=﹣2,c=﹣1,所以f(x)=x2﹣2x﹣1;
(2)g(x)=f(2x)﹣m2x+1=![]() ,
,
设t=2x,t∈[1,2],
∴g(t)=t2﹣(2m+2)t﹣1=[t﹣(m+1)]2﹣(m2+2m+2),
①当m+1>2,即m>1时,g(t)=t2﹣(2m+2) t﹣1在[1,2]减函数,当t=2时,g(t)min=﹣4m﹣1,
②当m+1<1,即m<0时,g(t)=t2﹣(2m+2)t﹣1在[1,2]增函数,当t=1时,g(t)min=﹣2m﹣2,
③当0≤m≤1时,当t=m+1时,g(t)min=﹣(m2+2m+2),
综上所述:g(x)min=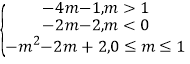 .
.

练习册系列答案
相关题目


