Question

【题目】已知二次函数.

（1）若是的两个不同的根，是否存在实数，使成立？若存在，求的值；若不存在，请说明理由.

（2）设，函数已知方程恰有3个不同的根.

（ⅰ）求的取值范围；

（ⅱ）设分别是这3个根中的最小值与最大值，求的最大值.

Answer 1

【答案】（1）不存在，理由见详解；（2）（ⅰ）；（ⅱ）.

【解析】

（1）由韦达定理，可得的取值；由，进行取舍；

（2）（ⅰ）构造函数，把有3个根，转化为与直线有三个交点的问题，数形结合处理；

（ii）分别解得和，进而构造函数，求其最大值.

（1）依题意可知，.假设存在实数，使成立.

因为有两个不同的根，

所以，解得.

由韦达定理得，

所以，

解得，而，故不存在.

（2）因为，设，则

当时，，当时，.

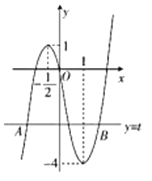
（ⅰ）作出的图象，如图所示，所以.

（ⅱ）设直线与此图象的最左边和最右边的交点分别为.

由，得；

由，得，

所以.

因为，

所以当时，取得最大值.

故的最大值为.