Question

【题目】某厂能够生产甲、乙两种产品，已知生产这两种产品每吨所需的煤、电以及每吨的产值分别是：

	用煤（t）	用电（kw）	产值（千元）
甲种产品	70	20	80
乙种产品	30	50	110

如果该厂每月至多供煤560t，供电450kw，问如何安排生产，才能使该厂月产值最大？月产值是多少？

Answer 1

【答案】安排甲月产，乙月产时，该厂月产值最大，最大值为1170千元．

【解析】

根据题意得到不等式组和目标函数，画出可行域，根据目标函数的几何意义得到最值。

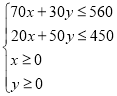设月产甲，乙，则，月产值，

上述不等式组所表示的平面区域如图所示的阴影部分，

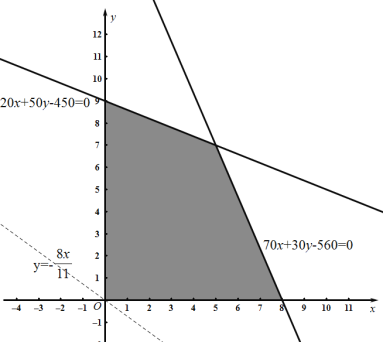
求的最大值问题转化为求在轴上截距的最大值．

由，解得，

即直线与直线的交点坐标是．

先作直线，平移可知当经过点时截距最大．

所以当，时，．

即安排甲月产，乙月产时，该厂月产值最大，最大值为1170千元．