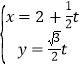题目内容
【题目】有人玩掷硬币走跳棋的游戏,已知硬币出现正反面为等可能性事件,棋盘上标有第0站,第1站,第2站,……,第100站.一枚棋子开始在第0站,棋手每掷一次硬币,棋子向前跳动一次,若掷出正面,棋向前跳一站(从k到![]() ),若掷出反面,棋向前跳两站(从k到
),若掷出反面,棋向前跳两站(从k到![]() ),直到棋子跳到第99站(胜利大本营)或跳到第100站(失败集中营)时,该游戏结束.设棋子跳到第n站概率为
),直到棋子跳到第99站(胜利大本营)或跳到第100站(失败集中营)时,该游戏结束.设棋子跳到第n站概率为![]() .
.
(1)求![]() ,
,![]() ,
,![]() 的值;
的值;
(2)求证:![]() ,其中
,其中![]() ,
,![]() ;
;
(3)求![]() 及
及![]() 的值.
的值.
【答案】(1)![]() .
.![]() .
.![]() .(2)见解析;(3)
.(2)见解析;(3)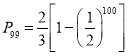 ,
, .
.
【解析】
(1)分析投掷硬币的情况,再分别计算即可.
(2)根据棋子跳到第![]() 站情况有且仅有①棋子先到第
站情况有且仅有①棋子先到第![]() 站,又掷出反面,②棋子先到第
站,又掷出反面,②棋子先到第![]() 站,又掷出正面,两种情况,再求出递推公式再化简证明即可.
站,又掷出正面,两种情况,再求出递推公式再化简证明即可.
(3)根据(2)可知数列![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列得到
的等比数列得到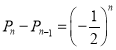 ,再累加求和求出
,再累加求和求出![]() 即可求解
即可求解![]() 及
及![]() .
.
(1)棋子开始在第0站为必然事件,∴![]() .
.
第一次掷硬币出现正面,棋子跳到第1站,其概率为![]() ,∴
,∴![]() .
.
棋子跳到第2站应从如下两方面考虑:
①前两次掷硬币都出现正面,其概率为![]() ;
;
②第一次掷硬币出现反面,其概率为![]() .
.
∴![]() .
.
(2)证明:棋子跳到第n(![]() )站的情况是下列两种,而且也只有两种:
)站的情况是下列两种,而且也只有两种:
①棋子先到第![]() 站,又掷出反面,其概率为
站,又掷出反面,其概率为![]() ;
;
②棋子先到第![]() 站,又掷出正面,其概率为
站,又掷出正面,其概率为![]() .
.
∴![]() .
.
∴![]() .
.
(3)由(2)知,当![]() 时,数列
时,数列![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列.
的等比数列.
∴![]() ,
,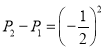 ,
,
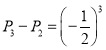 ,…,
,…,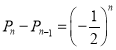 .
.
以上各式相加,得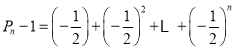 ,
,
∴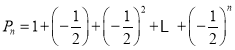
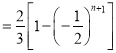
![]() .
.
∴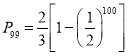 ,
,
 .
.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
【题目】某厂能够生产甲、乙两种产品,已知生产这两种产品每吨所需的煤、电以及每吨的产值分别是:
用煤(t) | 用电(kw) | 产值(千元) | |
甲种产品 | 70 | 20 | 80 |
乙种产品 | 30 | 50 | 110 |
如果该厂每月至多供煤560t,供电450kw,问如何安排生产,才能使该厂月产值最大?月产值是多少?