题目内容
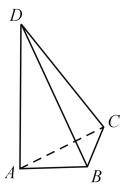
【题目】如图,AD与BC是四面体ABCD中互相垂直的棱,BC=2. 若AD=2c,且AB+BD=AC+CD=2a,其中a、c为常数,则四面体ABCD的体积的最大值是 .
【答案】![]()
【解析】


作BE⊥AD于E,连接CE,则AD⊥平面BEC,所以CE⊥AD,由题设,B与C都是在以AD为焦距的椭球上,且BE、CE都垂直于焦距AD,所以BE=CE. 取BC中点F,
连接EF,则EF⊥BC,EF=2,![]() ,四面体ABCD的体积
,四面体ABCD的体积![]() ,显然,当E在AD中点,即B是短轴端点时,BE有最大值为b=
,显然,当E在AD中点,即B是短轴端点时,BE有最大值为b=![]() ,所以
,所以![]() .
.
[评注] 本题把椭圆拓展到空间,对缺少联想思维的考生打击甚大!当然,作为填空押轴题,区分度还是要的,不过,就抢分而言,胆大、灵活的考生也容易找到突破点:AB=BD(同时AC=CD),从而致命一击,逃出生天!

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
【题目】火把节是彝族、白族、纳西族、基诺族、拉祜族等民族的古老传统节日,有着深厚的民俗文化内涵,被称为“东方的狂欢节”凉山州旅游局为了解民众对火把节知识的知晓情况,对西昌市区 A,B 两小区的部分居民开展了问卷调查,他们得分(满分100分)数据,统计结果如下:
A小区 | ||||
得分范围/分 |
|
|
|
|
频率 |
|
|
|
|
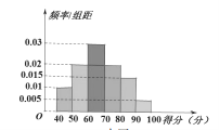
B小区
(1)以每组数据的中点值作为该组数据的代表,求B小区的平均分;
(2)若A小区得分在![]() 内的人数为
内的人数为![]() 人,B小区得分在
人,B小区得分在![]() 内的人数为
内的人数为![]() 人,求在 A,B 两小区中所有参加问卷调查的居民中得分不低于
人,求在 A,B 两小区中所有参加问卷调查的居民中得分不低于![]() 分的频率;
分的频率;