题目内容
【题目】设![]() 为实数,函数
为实数,函数![]() .
.
(1)当![]() 时,求
时,求![]() 的单调区间;
的单调区间;
(2)求![]() 在
在![]() 上的极大值与极小值.
上的极大值与极小值.
【答案】(1)单调区间有![]() ;(2)当
;(2)当![]() 时,
时,![]() 的极大值是
的极大值是![]() ,极小值是
,极小值是![]() ;当
;当![]() 时,
时,![]() 无极值;当
无极值;当![]() 时,
时,![]() 的极大值是
的极大值是![]() ,极小值是
,极小值是![]() .
.
【解析】
(1)当![]() 时,求出
时,求出![]() ,求解
,求解![]() ,即可得出结论;
,即可得出结论;
(2)求出![]() ,进而得到
,进而得到![]() 的根,按照根的大小对
的根,按照根的大小对![]() 分类讨论,求出单调区间,即可求解.
分类讨论,求出单调区间,即可求解.
(1)当![]() 时,
时,![]()
![]()
当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上单调递减.
上单调递减.
所以![]() 的单调区间有
的单调区间有![]() ;
;
(2)![]()
![]() 或
或![]() ,
,
当![]() 时,
时,![]()
所以![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() 在
在![]() 上无极值.
上无极值.
当![]() 时,随
时,随![]() 的变化
的变化![]() 变化如下:
变化如下:
|
|
|
|
|
|
| + | 0 | - | 0 | + |
| 增 | 极大值 | 减 | 极小值 | 增 |
所以![]() 的极大值是
的极大值是![]() ,
,
极小值是![]() ;
;
当![]() 时,随
时,随![]() 的变化
的变化![]() 变化如下:
变化如下:
|
|
|
|
|
|
| + | 0 | - | 0 | + |
| 增 | 极大值 | 减 | 极小值 | 增 |
所以![]() 的极小值是
的极小值是![]() ,
,
极大值是![]() .
.
综上,当![]() 时,
时,![]() 的极大值是
的极大值是![]() ,
,
极小值是![]() ;
;
当![]() 时,
时,![]() 无极值;
无极值;
当![]() 时,
时,![]() 的极大值是
的极大值是![]() ,
,
极小值是![]() .
.

 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案【题目】为响应国家“精准扶贫、精准脱贫”的号召,某贫困县在精准推进上下功夫,在精准扶贫上见实效.根据当地气候特点大力发展中医药产业,药用昆虫的使用相应愈来愈多,每年春暖以后到寒冬前,昆虫大量活动与繁殖,易于采取各种药用昆虫.已知一只药用昆虫的产卵数y(单位:个)与一定范围内的温度x(单位:℃)有关,于是科研人员在3月份的31天中随机选取了5天进行研究,现收集了该种药物昆虫的5组观察数据如表:
日期 | 2日 | 7日 | 15日 | 22日 | 30日 |
温度 | 10 | 11 | 13 | 12 | 8 |
产卵数y/个 | 22 | 24 | 29 | 25 | 16 |
(1)从这5天中任选2天,记这2天药用昆虫的产卵数分别为m,n,求“事件m,n均不小于24”的概率?
(2)科研人员确定的研究方案是:先从这5组数据中任选2组,用剩下的3组数据建立线性回归方程,再对被选取的2组数据进行检验.
①若选取的是3月2日与3月30日这2组数据,请根据3月7日、15日和22日这三组数据,求出y关于x的线性回归方程?
②若由线性回归方程得到的估计数据与所选出的检验数据的差的绝对值均不超过2个,则认为得到的线性回归方程是可靠的,试问①中所得的线性回归方程是否可靠?
附公式:![]() ,
,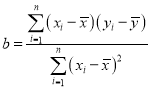
【题目】已知椭圆![]() :
:![]() 的左右焦点分别为
的左右焦点分别为![]() ,
,![]() ,离心率为
,离心率为![]() ,过
,过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() 周长为8.
周长为8.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)是否存在直线![]() ,使以
,使以![]() 为直径的圆经过坐标原点
为直径的圆经过坐标原点![]() ,若存在求出直线
,若存在求出直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
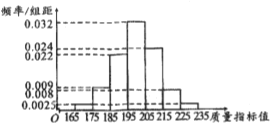
【题目】电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众进行调查,其中女性有55名.下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图;
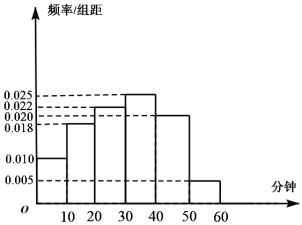
将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”,已知“体育迷”中有10名女性.
(Ⅰ)根据已知条件完成下面的![]() 列联表,并据此资料你是否认为“体育迷”与性别
列联表,并据此资料你是否认为“体育迷”与性别
有关?
非体育迷 | 体育迷 | 合计 | |
男 | |||
女 | |||
合计 |
(Ⅱ)将日均收看该体育项目不低于50分钟的观众称为“超级体育迷”,已知“超级体育迷”中有2名女性,若从“超级体育迷”中任意选取2人,求至少有1名女性观众的概率.
| 0.05 | 0.01 |
k | 3.841 | 6.635 |
附![]()