题目内容
(本题满分15分)
已知函数f (x )=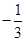 ax 3 + x2 + 2 ( a ≠ 0 ) .
ax 3 + x2 + 2 ( a ≠ 0 ) .
(Ⅰ) 试讨论函数f (x )的单调性;
(Ⅱ) 若a>0,求函数f (x ) 在[1,2]上的最大值.
解: (1) ①当a>0时, f(x)在(-∞,0),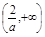 上是减函数,在
上是减函数,在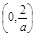 上是增函数.
上是增函数.
②当a<0时, f(x)在(-∞, 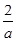 ),(0, +∞)上是增函数,在(
),(0, +∞)上是增函数,在(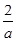 ,0)上是减函数.
,0)上是减函数.
(2)当0<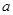 <1时,f(x)的最大值为3-
<1时,f(x)的最大值为3-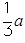 ,
,
当1≤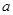 ≤2时,f(x)的最大值为
≤2时,f(x)的最大值为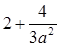 ,
,
当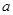 >2时,f(x)的最大值为
>2时,f(x)的最大值为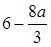 .
.
解析

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
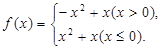 是奇函数。
是奇函数。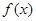 的定义域是
的定义域是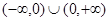 ,且
,且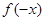 =
=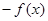 .已知当x>0时
.已知当x>0时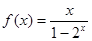
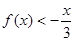 .
. ,曲线
,曲线 在点
在点 处的切线方程为
处的切线方程为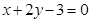 。
。 、
、 的值;
的值;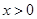 ,且
,且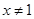 时,
时,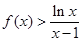 .
. 定义域为
定义域为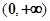 ,且满足
,且满足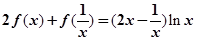 .
.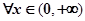 ,
,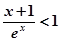 。
。  。求证:
。求证: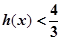 .
.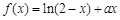 在(0,1)内是增函数.
在(0,1)内是增函数. 的取值范围;
的取值范围;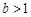 ,求证:
,求证: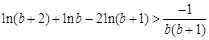 .
.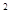 +4x+3,g(x)为一次函数,若f(g(x))=x
+4x+3,g(x)为一次函数,若f(g(x))=x
 的定义域
的定义域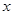 ,设
,设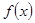 取
取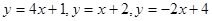 三个函数中的最小值,用分段函数写出
三个函数中的最小值,用分段函数写出