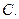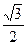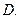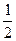题目内容
(本题满分14分)
已知椭圆C: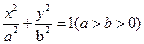 过点
过点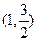 ,且长轴长等于4.
,且长轴长等于4.
(Ⅰ)求椭圆C的方程;
(Ⅱ)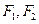 是椭圆C的两个焦点,⊙O是以F1F2为直径的圆,直线l: y=kx+m与⊙O相切,并与椭圆C交于不同的两点A、B,若
是椭圆C的两个焦点,⊙O是以F1F2为直径的圆,直线l: y=kx+m与⊙O相切,并与椭圆C交于不同的两点A、B,若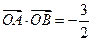 ,求
,求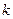 的值.
的值.
已知椭圆C:
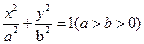 过点
过点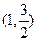 ,且长轴长等于4.
,且长轴长等于4.(Ⅰ)求椭圆C的方程;
(Ⅱ)
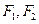 是椭圆C的两个焦点,⊙O是以F1F2为直径的圆,直线l: y=kx+m与⊙O相切,并与椭圆C交于不同的两点A、B,若
是椭圆C的两个焦点,⊙O是以F1F2为直径的圆,直线l: y=kx+m与⊙O相切,并与椭圆C交于不同的两点A、B,若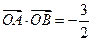 ,求
,求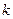 的值.
的值.(Ⅰ)
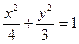
(Ⅱ)

解:(Ⅰ)由题意椭圆的长轴2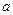 =4,得a=2, -------------------------1分
=4,得a=2, -------------------------1分
 点
点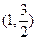 在椭圆上,
在椭圆上, ----------3分
----------3分
∴椭圆的方程为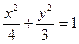 -------------------------------5分
-------------------------------5分
(Ⅱ)由直线l与圆O相切得 ---------------6分
---------------6分
设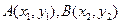 ,
,
由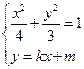 消去
消去 ,整理得
,整理得 ------7分
------7分
由题可知圆O在椭圆内,所以直线必与椭圆相交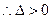 -------------------------8分
-------------------------8分
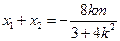
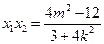 --------------------------------------9分
--------------------------------------9分
 =
=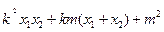
=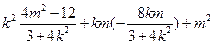 =
= -------------------10分
-------------------10分
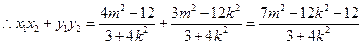 ----------------------11分
----------------------11分
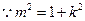
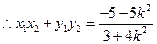 ---
--- -----------------12分
-----------------12分
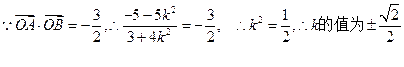 -------14分
-------14分
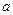 =4,得a=2, -------------------------1分
=4,得a=2, -------------------------1分 点
点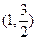 在椭圆上,
在椭圆上, ----------3分
----------3分∴椭圆的方程为
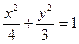 -------------------------------5分
-------------------------------5分(Ⅱ)由直线l与圆O相切得
 ---------------6分
---------------6分设
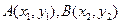 ,
,由
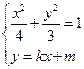 消去
消去 ,整理得
,整理得 ------7分
------7分由题可知圆O在椭圆内,所以直线必与椭圆相交
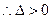 -------------------------8分
-------------------------8分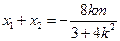
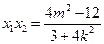 --------------------------------------9分
--------------------------------------9分 =
=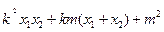
=
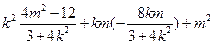 =
= -------------------10分
-------------------10分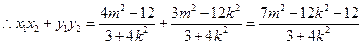 ----------------------11分
----------------------11分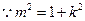
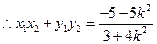 ---
--- -----------------12分
-----------------12分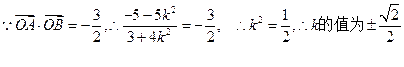 -------14分
-------14分
练习册系列答案
相关题目
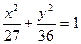 有相同焦点,且经过点
有相同焦点,且经过点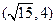 .
.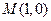 作斜率为1的直线交双曲线于
作斜率为1的直线交双曲线于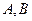 两点,求
两点,求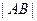 .
.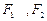 分别是椭圆C:
分别是椭圆C: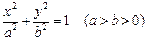 的左右焦点,
的左右焦点,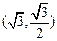 到
到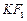 的中点B的轨迹方程。
的中点B的轨迹方程。 )设点P是椭圆C 上的任意一点,过原点的直线L与椭圆相交于M,N两点,当直线PM ,PN的斜率都存在,并记为
)设点P是椭圆C 上的任意一点,过原点的直线L与椭圆相交于M,N两点,当直线PM ,PN的斜率都存在,并记为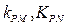 试探究
试探究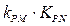 的值是否与点P及直线L有关,并证明你的结论。
的值是否与点P及直线L有关,并证明你的结论。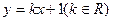 与椭圆
与椭圆

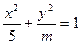 恒有公共点。则实数m的取值范围是( )
恒有公共点。则实数m的取值范围是( )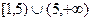
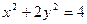 ,则以
,则以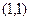 为中点的弦的长度为
为中点的弦的长度为 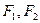 为椭圆
为椭圆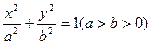 的两个焦点,过
的两个焦点,过 作椭圆的弦
作椭圆的弦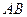 ,若
,若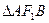 的周长为16,离心率为
的周长为16,离心率为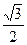 ,则椭圆的方程为( )
,则椭圆的方程为( )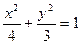
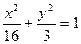
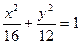
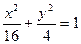
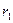 ,
,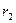 ,则卫星轨道的离心率为 .
,则卫星轨道的离心率为 .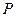 在椭圆
在椭圆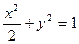 上,
上,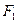 、
、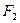 分别是椭圆的两焦点,且
分别是椭圆的两焦点,且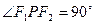 ,则
,则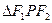 的面积是 ( )
的面积是 ( )  2
2  1
1