题目内容
对于定义域为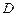 的函数
的函数 ,若有常数M,使得对任意的
,若有常数M,使得对任意的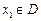 ,存在唯一的
,存在唯一的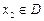 满足等式
满足等式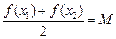 ,则称M为函数
,则称M为函数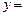 f (x)的“均值”.
f (x)的“均值”.
(1)判断1是否为函数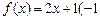 ≤
≤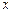 ≤
≤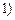 的“均值”,请说明理由;
的“均值”,请说明理由;
(2)若函数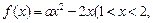
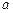 为常数)存在“均值”,求实数a的取值范围;
为常数)存在“均值”,求实数a的取值范围;
(3)若函数 是单调函数,且其值域为区间I.试探究函数
是单调函数,且其值域为区间I.试探究函数 的“均值”情况(是否存在、个数、大小等)与区间I之间的关系,写出你的结论(不必证明).
的“均值”情况(是否存在、个数、大小等)与区间I之间的关系,写出你的结论(不必证明).
说明:对于(3),将根据结论的完整性与一般性程度给予不同的评分
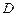 的函数
的函数 ,若有常数M,使得对任意的
,若有常数M,使得对任意的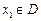 ,存在唯一的
,存在唯一的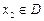 满足等式
满足等式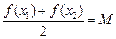 ,则称M为函数
,则称M为函数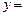 f (x)的“均值”.
f (x)的“均值”.(1)判断1是否为函数
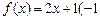 ≤
≤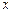 ≤
≤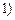 的“均值”,请说明理由;
的“均值”,请说明理由;(2)若函数
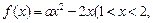
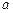 为常数)存在“均值”,求实数a的取值范围;
为常数)存在“均值”,求实数a的取值范围;(3)若函数
 是单调函数,且其值域为区间I.试探究函数
是单调函数,且其值域为区间I.试探究函数 的“均值”情况(是否存在、个数、大小等)与区间I之间的关系,写出你的结论(不必证明).
的“均值”情况(是否存在、个数、大小等)与区间I之间的关系,写出你的结论(不必证明).说明:对于(3),将根据结论的完整性与一般性程度给予不同的评分
解:(1)对任意的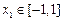 ,有
,有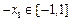 ,
,
当且仅当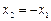 时,有
时,有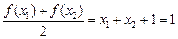 ,
,
故存在唯一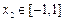 ,满足
,满足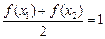
 , ……………………2分
, ……………………2分
所以1是函数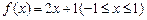 的“均值”. ……………………4分
的“均值”. ……………………4分
(另法:对任意的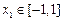 ,有
,有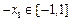 ,令
,令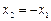 ,
,
则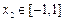 ,且
,且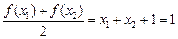 ,
,
若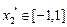 ,且
,且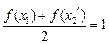 ,则有
,则有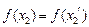 ,可得
,可得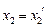 ,
,
故存在唯一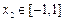 ,满足
,满足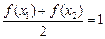 , ……………………2分
, ……………………2分
所以1是函数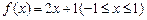 的“
的“ 均值”. ……………………4分)
均值”. ……………………4分)
(2)当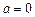 时,
时,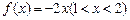 存在“均值”,且“均值”为
存在“均值”,且“均值”为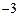 ;…………5分
;…………5分
当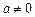 时,由
时,由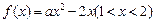 存在均值,可知对任意的
存在均值,可知对任意的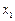 ,
,
都有唯一的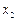 与之对应,从而有
与之对应,从而有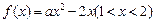 单调,
单调,
故有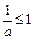 或
或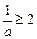 ,解得
,解得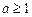 或
或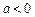 或
或 , ……………………9分
, ……………………9分
综上,a的取值范围是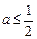 或
或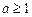 . ……………………10分
. ……………………10分
(另法:分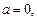
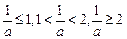 四种情形
四种情形 进行讨论)
进行讨论)
(3)①当I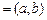 或
或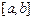 时,函数
时,函数 存在唯一的“均值”.
存在唯一的“均值”.
这时函数 的“均值”为
的“均值”为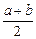 ; …………………12分
; …………………12分
②当I为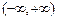 时,函数
时,函数 存在无数多个“均值”.
存在无数多个“均值”.
这时任意实数均为函数 的“均值”; ……………………14分
的“均值”; ……………………14分
③当I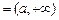 或
或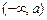 或
或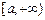 或
或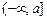 或
或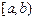 或
或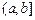 时,
时,
函数 不存在“均值”. ……………………16分
不存在“均值”. ……………………16分
[评分说明:若三种情况讨论完整且正确,但未用等价形式进行叙述,至多得6分;若三种情况讨论不完整,且未用等价形式叙述,至多得5分]
①当且仅当I形如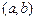 、
、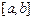 其中之一时,函数
其中之一时,函数 存在唯一的“均值”.
存在唯一的“均值”.
这时函数 的“均值”为
的“均值”为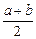 ; ……………………13分
; ……………………13分
②当且仅当I为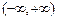 时,函数
时,函数 存在无数多个“均值”.
存在无数多个“均值”.
这时任意实数均为函数 的“均值”; ……………………16分
的“均值”; ……………………16分
③当且仅当I形如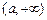 、
、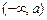 、
、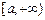 、
、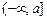 、
、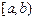 、
、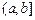 其中之一时,函数
其中之一时,函数 不存在“均值”. ……………………18分
不存在“均值”. ……………………18分
(另法:①当且仅当I为开区间或闭区间时,函数 存在唯一的“均值”.这时函数
存在唯一的“均值”.这时函数 的均值为区间I两端点的算术平均数; ……………………13分
的均值为区间I两端点的算术平均数; ……………………13分
②当且仅当I为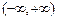 时,函数
时,函数 存在无数多个“均值”.这时任意实数均为函数
存在无数多个“均值”.这时任意实数均为函数 的“均值”; ……………………16分
的“均值”; ……………………16分
③当且仅当I为除去开区间、闭区间与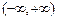 之外的其它区间时,函数
之外的其它区间时,函数 不存在“均值”. ……………………18分)
不存在“均值”. ……………………18分)
[评分说明:在情形①与②中,等价关系叙述正确但未正确求出函数“均值”,各扣1分]
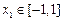 ,有
,有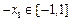 ,
,当且仅当
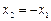 时,有
时,有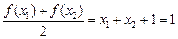 ,
, 故存在唯一
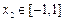 ,满足
,满足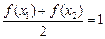
 , ……………………2分
, ……………………2分所以1是函数
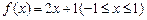 的“均值”. ……………………4分
的“均值”. ……………………4分(另法:对任意的
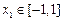 ,有
,有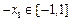 ,令
,令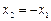 ,
,则
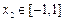 ,且
,且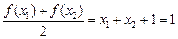 ,
, 若
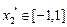 ,且
,且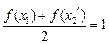 ,则有
,则有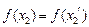 ,可得
,可得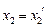 ,
,故存在唯一
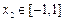 ,满足
,满足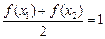 , ……………………2分
, ……………………2分所以1是函数
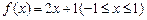 的“
的“ 均值”. ……………………4分)
均值”. ……………………4分)(2)当
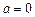 时,
时,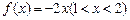 存在“均值”,且“均值”为
存在“均值”,且“均值”为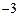 ;…………5分
;…………5分当
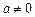 时,由
时,由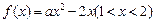 存在均值,可知对任意的
存在均值,可知对任意的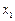 ,
,都有唯一的
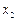 与之对应,从而有
与之对应,从而有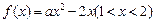 单调,
单调,故有
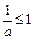 或
或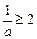 ,解得
,解得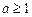 或
或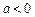 或
或 , ……………………9分
, ……………………9分综上,a的取值范围是
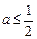 或
或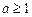 . ……………………10分
. ……………………10分(另法:分
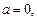
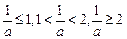 四种情形
四种情形 进行讨论)
进行讨论)(3)①当I
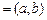 或
或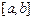 时,函数
时,函数 存在唯一的“均值”.
存在唯一的“均值”.这时函数
 的“均值”为
的“均值”为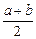 ; …………………12分
; …………………12分②当I为
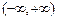 时,函数
时,函数 存在无数多个“均值”.
存在无数多个“均值”.这时任意实数均为函数
 的“均值”; ……………………14分
的“均值”; ……………………14分③当I
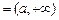 或
或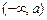 或
或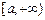 或
或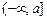 或
或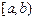 或
或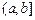 时,
时,函数
 不存在“均值”. ……………………16分
不存在“均值”. ……………………16分[评分说明:若三种情况讨论完整且正确,但未用等价形式进行叙述,至多得6分;若三种情况讨论不完整,且未用等价形式叙述,至多得5分]
①当且仅当I形如
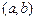 、
、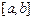 其中之一时,函数
其中之一时,函数 存在唯一的“均值”.
存在唯一的“均值”.这时函数
 的“均值”为
的“均值”为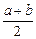 ; ……………………13分
; ……………………13分②当且仅当I为
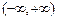 时,函数
时,函数 存在无数多个“均值”.
存在无数多个“均值”.这时任意实数均为函数
 的“均值”; ……………………16分
的“均值”; ……………………16分③当且仅当I形如
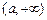 、
、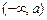 、
、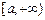 、
、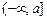 、
、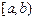 、
、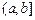 其中之一时,函数
其中之一时,函数 不存在“均值”. ……………………18分
不存在“均值”. ……………………18分(另法:①当且仅当I为开区间或闭区间时,函数
 存在唯一的“均值”.这时函数
存在唯一的“均值”.这时函数 的均值为区间I两端点的算术平均数; ……………………13分
的均值为区间I两端点的算术平均数; ……………………13分②当且仅当I为
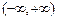 时,函数
时,函数 存在无数多个“均值”.这时任意实数均为函数
存在无数多个“均值”.这时任意实数均为函数 的“均值”; ……………………16分
的“均值”; ……………………16分③当且仅当I为除去开区间、闭区间与
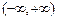 之外的其它区间时,函数
之外的其它区间时,函数 不存在“均值”. ……………………18分)
不存在“均值”. ……………………18分)
[评分说明:在情形①与②中,等价关系叙述正确但未正确求出函数“均值”,各扣1分]
略

练习册系列答案
相关题目
 的值域为
的值域为 ,则
,则 的最大值为( )
的最大值为( )



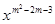 ,当x∈(0, +∞)时为减函数,则实数m的值是
,当x∈(0, +∞)时为减函数,则实数m的值是 
 ,则函数
,则函数 的最小值为( )
的最小值为( )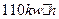 B.
B.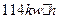 C.
C.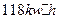 D.
D.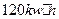
 的图像大致是 ( )
的图像大致是 ( )
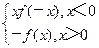 ,则{x|F(x)>0}=
,则{x|F(x)>0}=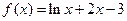 零点的个数为
零点的个数为