题目内容
如图,在△ABC中,∠ABC=90°,∠A=30。,斜边AC上的中线BD=2,现沿BD将△BCD折起成三棱锥C-ABD,已知G是线段BD的中点,E,F分别是CG,AG的中点.
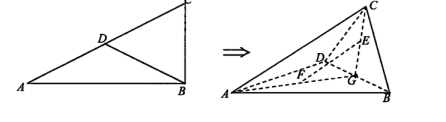
(1)求证:EF//平面ABC;
(2)三棱锥C—ABD中,若棱AC=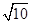 ,求三棱锥A一BCD的体积.
,求三棱锥A一BCD的体积.

(1)求证:EF//平面ABC;
(2)三棱锥C—ABD中,若棱AC=
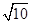 ,求三棱锥A一BCD的体积.
,求三棱锥A一BCD的体积.(1)证明过程详见解析;(2) .
.
 .
.试题分析:本题主要以平面图形的翻折为几何背景,考查三棱锥中的线线平行、线面平行、线面垂直以及三棱锥的体积等数学知识,考查学生的空间想象能力和逻辑推理能力.第一问,由题意得EF//AC,利用线面平行的判定得线面平行;第二问,在
 中,利用余弦定理可以求出AG的边长,在
中,利用余弦定理可以求出AG的边长,在 中,利用三个边长的关系,可判断出
中,利用三个边长的关系,可判断出 ,所以利用线面垂直的判定可以得到
,所以利用线面垂直的判定可以得到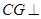 平面ABD,所以CG是锥体的高,利用等体积法将
平面ABD,所以CG是锥体的高,利用等体积法将 转化为
转化为 ,从而求出锥体的体积.
,从而求出锥体的体积.试题解析:(1) 证明:⑴ EF是
 的中位线
的中位线 EF//AC 3分
EF//AC 3分又AC
 平面ABC EF
平面ABC EF 平面ABC
平面ABC EF//平面ABC 6分
EF//平面ABC 6分⑵在
 中,
中, ,由余弦定理得:
,由余弦定理得: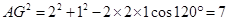 , 8分
, 8分而



即CG
 AG,又CG
AG,又CG BD
BD 

 平面ABD 10分
平面ABD 10分
 12分
12分
练习册系列答案
相关题目









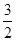

 π
π


