题目内容
【题目】如图所示，圆锥SO的轴截面△SAB是边长为4的正三角形，M为母线SB的中点，过直线AM作平面β⊥面SAB，设β与圆锥侧面的交线为椭圆C，则椭圆C的短半轴长为（ ）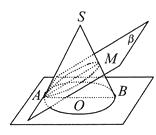 
A.
B.
C.
D.
【答案】A
【解析】解答：过椭圆C作平行于圆锥底面的截面（圆形），交AS，BS于R，T，交椭圆C于两点P，Q，则P，Q即是椭圆短半轴顶点，在所作的圆中，RT为直径，如图，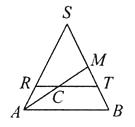 
因为轴截面△SAB是边长为4的正三角形，C为AM的中点，所以TC= 
AB=2，RC= 
AB=1，，因为PQ⊥RT，所以PC＝CQ，所以利用相交弦定理可得：PC·CQ＝TC·RC，所以PC= 
.所以橄圆C的短半轴为 .
分析：本题主要考查了平面与圆锥面的截线，解决问题的关键是根据平面与圆锥面的截线的性质结合所给几何关系利用相交弦的性质分析计算即可
练习册系列答案
阅读快车系列答案
相关题目
【题目】某工厂有25周岁以上（含25周岁）工人300名，25周岁以 下工人200名.为研究工人的日平均生产量是否与年龄有关.现采用分层抽样的方法，从中抽取了100名工人，先统计了他们某月的日平均生产件数，然后按工人年龄在“ 25周岁以上（含25周岁）”和“25周岁以下”分为两组，再将两组工人的日平均生产件数分成5组： 
， 
， 
， 
， 
分别加以统计，得到如图所示的频率分布直方图.
附表：
P（ | 0.100 | 0 .010 | 0.001 |
k | 2.706 | 6.635 | 10.828 |
，（其中 
）
（1）从样本中日平均生产件数不足60件的工人中随机抽取2人，求至少抽到一名“25周岁以下组”工人的频率.
（2）规定日平均生产件数不少于80件者为“生产能手”，请你根据已知条件完成 
的列联表，并判断是否有 
的把握认为“生产能手与工人所在的年龄组有关”？
