题目内容
在一个圆形波浪实验水池的中心有三个振动源,假如不计其它因素,在t秒内,它们引发的水面波动可分别由函数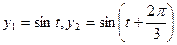 和
和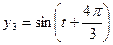 描述。如果两个振动源同时启动,则水面波动由两个函数的和表达。在某一时刻使这三个振动源同时开始工作,那么,原本平静的水面将呈现怎样的状态,请说明理由
描述。如果两个振动源同时启动,则水面波动由两个函数的和表达。在某一时刻使这三个振动源同时开始工作,那么,原本平静的水面将呈现怎样的状态,请说明理由
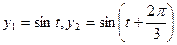 和
和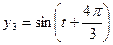 描述。如果两个振动源同时启动,则水面波动由两个函数的和表达。在某一时刻使这三个振动源同时开始工作,那么,原本平静的水面将呈现怎样的状态,请说明理由
描述。如果两个振动源同时启动,则水面波动由两个函数的和表达。在某一时刻使这三个振动源同时开始工作,那么,原本平静的水面将呈现怎样的状态,请说明理由同解析
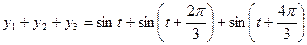
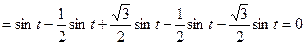
即三个振动源产生的振动被相互抵消,所以,原本平静的水面仍保持平静。

练习册系列答案
相关题目
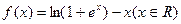 有下列性质:“若
有下列性质:“若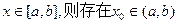 ,使得
,使得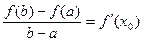 ”成立。
”成立。 唯一;
唯一; 图象上三个不同的点,试判断△ABC的形状,并说明理由。
图象上三个不同的点,试判断△ABC的形状,并说明理由。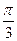 ,3)平移得到图象F′,若F′的一条对称轴是直线x=
,3)平移得到图象F′,若F′的一条对称轴是直线x=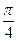 ,则θ的一个可能取值是
,则θ的一个可能取值是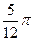
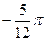

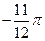
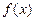 是定义在
是定义在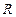 上的偶函数,当
上的偶函数,当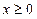 时,
时,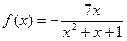 .
.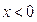 时
时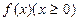 的单调区间,并证明你的结论;
的单调区间,并证明你的结论;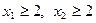 且
且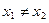 ,证明:
,证明: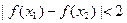 .
.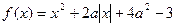 的零点有且只有一个,求
的零点有且只有一个,求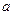 的值
的值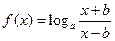
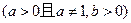 .
.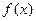 的定义域;
的定义域;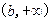 上的单调性.
上的单调性.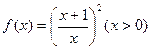 .
.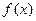 的反函数
的反函数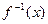 ;
;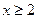 时,不等式
时,不等式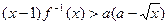 恒成立,试求实数
恒成立,试求实数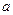 的范围.
的范围.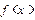 是定义在
是定义在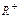 上的减函数,并且满足
上的减函数,并且满足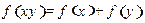 ,
,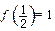 .
.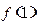 的值;
的值;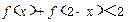 .
.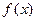 与产量
与产量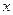 之间的关系式为
之间的关系式为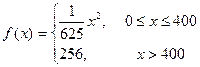 ,每件产品的售价
,每件产品的售价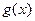 与产量
与产量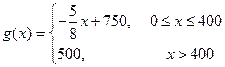 .
. 与产量
与产量