题目内容
(本小题满分14分)已知函数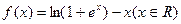 有下列性质:“若
有下列性质:“若
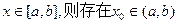 ,使得
,使得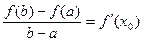 ”成立。
”成立。
(1)利用这个性质证明 唯一;
唯一;
(2)设A、B、C是函数 图象上三个不同的点,试判断△ABC的形状,并说明理由。
图象上三个不同的点,试判断△ABC的形状,并说明理由。
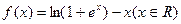 有下列性质:“若
有下列性质:“若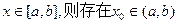 ,使得
,使得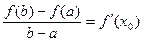 ”成立。
”成立。(1)利用这个性质证明
 唯一;
唯一;(2)设A、B、C是函数
 图象上三个不同的点,试判断△ABC的形状,并说明理由。
图象上三个不同的点,试判断△ABC的形状,并说明理由。(1)见解析(2)钝角三角形
证明:假设存在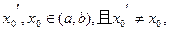 使得
使得
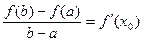
∴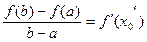
∵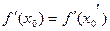 …………………………2分
…………………………2分
∴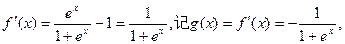
∴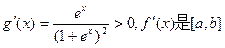 上的单调增函数。……………………5分
上的单调增函数。……………………5分
∴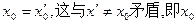 是唯一的。……………………6分
是唯一的。……………………6分
(2)设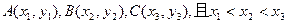
∵
∴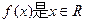 上的单调减函数。
上的单调减函数。
∴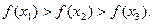 ……………………8分
……………………8分
∵
∴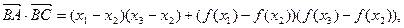 …………10分
…………10分
∵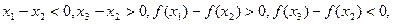 …………12分
…………12分
∴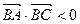
∴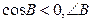 为钝角
为钝角
∴△ABC为钝角三角形。
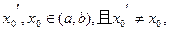 使得
使得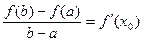
∴
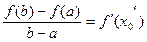
∵
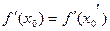 …………………………2分
…………………………2分∴
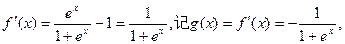
∴
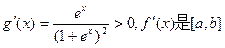 上的单调增函数。……………………5分
上的单调增函数。……………………5分∴
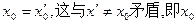 是唯一的。……………………6分
是唯一的。……………………6分(2)设
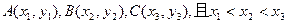
∵

∴
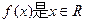 上的单调减函数。
上的单调减函数。∴
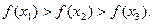 ……………………8分
……………………8分∵

∴
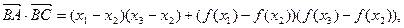 …………10分
…………10分∵
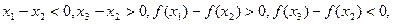 …………12分
…………12分∴
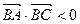
∴
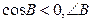 为钝角
为钝角∴△ABC为钝角三角形。

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
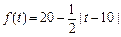 (元).
(元).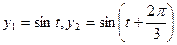 和
和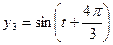 描述。如果两个振动源同时启动,则水面波动由两个函数的和表达。在某一时刻使这三个振动源同时开始工作,那么,原本平静的水面将呈现怎样的状态,请说明理由
描述。如果两个振动源同时启动,则水面波动由两个函数的和表达。在某一时刻使这三个振动源同时开始工作,那么,原本平静的水面将呈现怎样的状态,请说明理由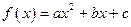 .
.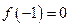 ,试判断函数
,试判断函数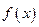 零点个数;
零点个数;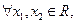 且
且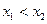 ,
,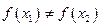 ,试证明
,试证明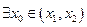 ,使
,使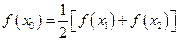 成立。
成立。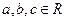 ,使
,使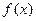 同时满足以下条件①对
同时满足以下条件①对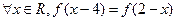 ,且
,且 ;②对
;②对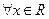 ,都有
,都有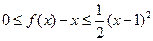 。若存在,求出
。若存在,求出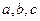 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。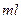 到110
到110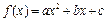 ,其中
,其中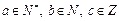 .
.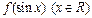 的最大值为2,最小值为-4,试求函数f(x)的最小值;
的最大值为2,最小值为-4,试求函数f(x)的最小值;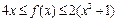 恒成立,且存在
恒成立,且存在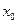 使得
使得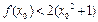 成立,求c的值.
成立,求c的值.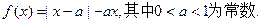
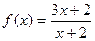 ,
,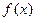 图象的对称中心;
图象的对称中心;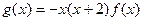 ,求
,求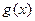 在区间
在区间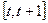 上的最大值
上的最大值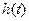 ;
;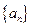 满足
满足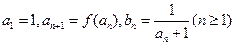 ,
,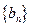 的通项公式
的通项公式
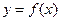 是二次函数,方程f(x)=0有两个相等的实根,且
是二次函数,方程f(x)=0有两个相等的实根,且