题目内容
如图,过抛物线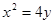 焦点的直线依次交抛物线与圆
焦点的直线依次交抛物线与圆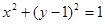 于点A、B、C、D,则
于点A、B、C、D,则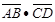 的值是( )
的值是( )
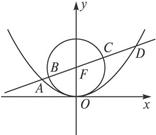
A.8 B.4 C.2 D.1
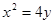 焦点的直线依次交抛物线与圆
焦点的直线依次交抛物线与圆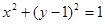 于点A、B、C、D,则
于点A、B、C、D,则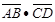 的值是( )
的值是( )
A.8 B.4 C.2 D.1
D
试题分析:利用特殊值法:过焦点的直线取
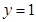 ,此时
,此时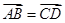 ,
,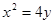 中令
中令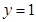 得
得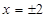 ,
,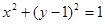 中令
中令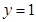 得
得 ,
, ,
,
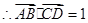
点评:选择题中利用特殊值,特殊位置求解简便易行

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
题目内容
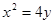 焦点的直线依次交抛物线与圆
焦点的直线依次交抛物线与圆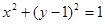 于点A、B、C、D,则
于点A、B、C、D,则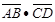 的值是( )
的值是( )
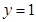 ,此时
,此时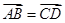 ,
,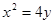 中令
中令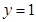 得
得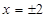 ,
,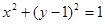 中令
中令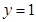 得
得 ,
, ,
,
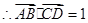

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案