题目内容
已知以双曲线C的两个焦点及虚轴的两个端点为原点的四边形中,有一个内角为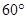 ,则双曲线C的离心率为 .
,则双曲线C的离心率为 .
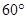 ,则双曲线C的离心率为 .
,则双曲线C的离心率为 .
试题分析:设双曲线C的焦点坐标是F1和F2,虚轴两个端点是B1和B2,则四边形F1B1F2B2为菱形.
①若∠B2F1B1=60°,则∠B2F1F2=30°.由勾股定理可知c=
 ,故双曲线C的离心率为e=
,故双曲线C的离心率为e= ;
;②若∠F1B2F2=60°,则∠F1B2B1=30°,由勾股定理可知b=
 c,不满足c>b,所以不成立.
c,不满足c>b,所以不成立.综上所述,双曲线C的离心率为
 。
。点评:解题时应该分∠B2F1B1=60°和∠F1B2F2=60°两种情况求出双曲线的离心率.但要注意a,b,c中c最大,根据此条进行验根,避免出现不必要的错误.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
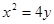 焦点的直线依次交抛物线与圆
焦点的直线依次交抛物线与圆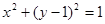 于点A、B、C、D,则
于点A、B、C、D,则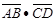 的值是( )
的值是( )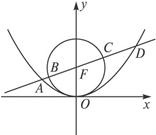
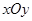 中,点
中,点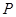 到两点
到两点 ,
,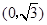 的距离之和等于
的距离之和等于 ,设点
,设点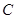 。
。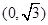 作两条互相垂直的直线
作两条互相垂直的直线 分别与曲线
分别与曲线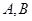 和
和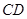 。
。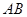 为直径的圆过能否过坐标原点,若能求出此时的
为直径的圆过能否过坐标原点,若能求出此时的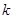 值,若不能说明理由;
值,若不能说明理由;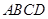 面积的取值范围。
面积的取值范围。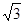 ) ,渐近线方程为
) ,渐近线方程为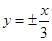 ,则此双曲线的方程为 _.
,则此双曲线的方程为 _.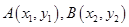 ,定义它们之间的一种“距离”:
,定义它们之间的一种“距离”: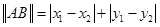 .给出下列三个命题:
.给出下列三个命题: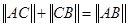 ;
;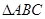 中,若∠C=90°,则
中,若∠C=90°,则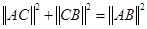 ;
;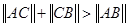 .
.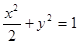 的右焦点作倾斜角为
的右焦点作倾斜角为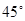 的直线
的直线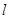 ,交椭圆于A、B两点,O为坐标原点,则
,交椭圆于A、B两点,O为坐标原点,则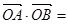 ( )
( )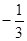

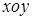 中,
中, 为椭圆
为椭圆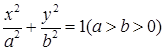 的
的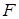 为其右焦点,直线
为其右焦点,直线 与直线
与直线 相交于点T,线段
相交于点T,线段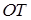 与椭圆的交点
与椭圆的交点 恰为线段
恰为线段
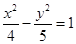 ,则离心率为 .
,则离心率为 .