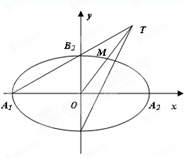
题目内容
如图,已知抛物线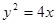 ,焦点为
,焦点为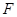 ,顶点为
,顶点为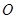 ,点
,点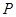 在抛物线上移动,
在抛物线上移动,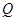 是
是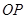 的中点,
的中点,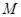 是
是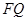 的中点,求点
的中点,求点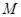 的轨迹方程.
的轨迹方程.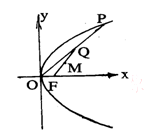
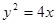 ,焦点为
,焦点为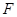 ,顶点为
,顶点为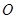 ,点
,点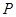 在抛物线上移动,
在抛物线上移动,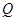 是
是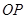 的中点,
的中点,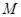 是
是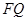 的中点,求点
的中点,求点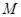 的轨迹方程.
的轨迹方程.

试题分析:设
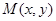 ,
, 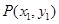 ,
, 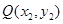 ,
,易求
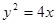 的焦点
的焦点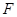 的坐标为(1,0), ……2分
的坐标为(1,0), ……2分∵
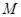 是
是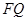 的中点,
的中点,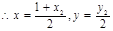
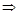
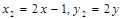 , ……6分
, ……6分又
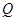 是
是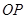 的中点,
的中点,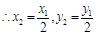
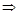
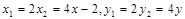 , ……10分 ∵P在抛物线
, ……10分 ∵P在抛物线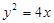 上,∴
上,∴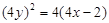 ,
,所以M点的轨迹方程为
 . ……12分
. ……12分点评:求轨迹方程时本着“求谁设谁”的原则,方法主要要相关点法、代人法等.

练习册系列答案
相关题目
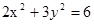 有两个交点 ( )
有两个交点 ( )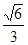 <k<
<k<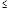 k
k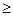
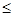 —
—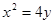 焦点的直线依次交抛物线与圆
焦点的直线依次交抛物线与圆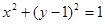 于点A、B、C、D,则
于点A、B、C、D,则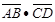 的值是( )
的值是( )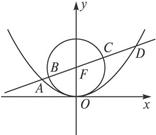
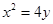 的准线方程为 .
的准线方程为 .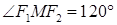 ,则双曲线离心率为
,则双曲线离心率为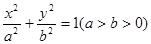 的两焦点为
的两焦点为 、
、 ,以
,以 为边作正三角形,若椭圆恰好平分该正三角形的另两边,则椭圆的离心率是( )
为边作正三角形,若椭圆恰好平分该正三角形的另两边,则椭圆的离心率是( )



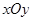 中,点
中,点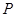 到两点
到两点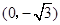 ,
,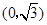 的距离之和等于
的距离之和等于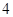 ,设点
,设点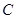 。
。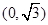 作两条互相垂直的直线
作两条互相垂直的直线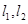 分别与曲线
分别与曲线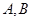 和
和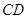 。
。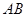 为直径的圆过能否过坐标原点,若能求出此时的
为直径的圆过能否过坐标原点,若能求出此时的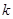 值,若不能说明理由;
值,若不能说明理由;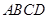 面积的取值范围。
面积的取值范围。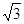 ) ,渐近线方程为
) ,渐近线方程为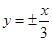 ,则此双曲线的方程为 _.
,则此双曲线的方程为 _.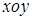 中,
中,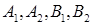 为椭圆
为椭圆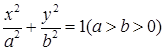 的
的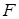 为其右焦点,直线
为其右焦点,直线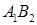 与直线
与直线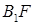 相交于点T,线段
相交于点T,线段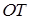 与椭圆的交点
与椭圆的交点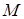 恰为线段
恰为线段