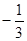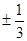题目内容
给出下列命题,其中正确命题的序号是 (填序号)。
(1)已知椭圆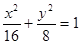 两焦点为
两焦点为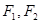 ,则椭圆上存在六个不同点
,则椭圆上存在六个不同点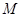 ,使得
,使得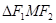 为直角三角形;
为直角三角形;
(2)已知直线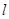 过抛物线
过抛物线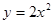 的焦点,且与这条抛物线交于
的焦点,且与这条抛物线交于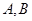 两点,则
两点,则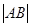 的最小值为2;
的最小值为2;
(3)若过双曲线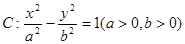 的一个焦点作它的一条渐近线的垂线,垂足为
的一个焦点作它的一条渐近线的垂线,垂足为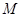 ,
,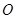 为坐标原点,则
为坐标原点,则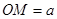 ;
;
(4)已知⊙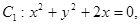 ⊙
⊙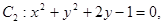 则这两圆恰有2条公切线。
则这两圆恰有2条公切线。
(1)已知椭圆
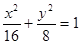 两焦点为
两焦点为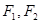 ,则椭圆上存在六个不同点
,则椭圆上存在六个不同点 ,使得
,使得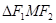 为直角三角形;
为直角三角形;(2)已知直线
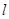 过抛物线
过抛物线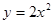 的焦点,且与这条抛物线交于
的焦点,且与这条抛物线交于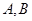 两点,则
两点,则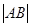 的最小值为2;
的最小值为2;(3)若过双曲线
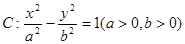 的一个焦点作它的一条渐近线的垂线,垂足为
的一个焦点作它的一条渐近线的垂线,垂足为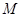 ,
,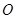 为坐标原点,则
为坐标原点,则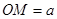 ;
;(4)已知⊙
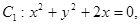 ⊙
⊙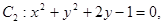 则这两圆恰有2条公切线。
则这两圆恰有2条公切线。( 1) ( 3)( 4)
试题分析:椭圆
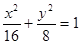 的两个焦点为F1(-2
的两个焦点为F1(-2 ,0),F2(2
,0),F2(2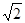 ,0),当F1M垂直于x 轴时,这样的点M有2个.当MF2垂直于x 轴时,这样的点M有2个.当∠F1MF2 为直角时,点M恰是椭圆短轴的端点(0,,2
,0),当F1M垂直于x 轴时,这样的点M有2个.当MF2垂直于x 轴时,这样的点M有2个.当∠F1MF2 为直角时,点M恰是椭圆短轴的端点(0,,2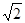 ),这样的点M有2个,综上,这个椭圆上存在六个不同的点M,使得△F1MF2为直角三角形,故①正确.
),这样的点M有2个,综上,这个椭圆上存在六个不同的点M,使得△F1MF2为直角三角形,故①正确.因为过抛物线y=2x2的焦点,且与这条抛物线交于A,B两点,则|AB|的最小值为抛物线的通径2p,由抛物线y=2x2的方程即x2=
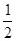 y 知,p=
y 知,p=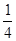 ,2p=
,2p=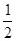 ,则|AB|的最小值为
,则|AB|的最小值为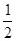 ,故②不正确.
,故②不正确.因为双曲线
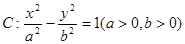 的一个焦点为(c,0),一条渐近线的方程 y=
的一个焦点为(c,0),一条渐近线的方程 y=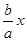 ,故垂线方程为 y-0=-
,故垂线方程为 y-0=-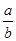 (x-c),它与渐近线 y=
(x-c),它与渐近线 y=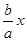 的交点M(
的交点M(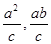 ),所以MO=a,故③正确.
),所以MO=a,故③正确.因为⊙C1:x2+y2+2x=0,即 (x+1)2+y2=1,表示圆心为(-1,0),半径等于1的圆;⊙C2:x2+y2+2y-1="0" 即,x2+(y+1)2=2,表示圆心为(0,-1),半径等于
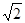 的圆.两圆的圆心距等于
的圆.两圆的圆心距等于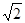 ,大于两圆的半径之差,小于两圆的半径之和,故两圆相交,故两圆的公切线有2条,故④正确.
,大于两圆的半径之差,小于两圆的半径之和,故两圆相交,故两圆的公切线有2条,故④正确.故答案为:①③④.
点评:掌握圆锥曲线的性质是解题的前提,灵活应用圆锥曲线的性质是解题的关键。属于中档题。

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
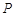 是椭圆
是椭圆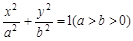 上的一动点,且
上的一动点,且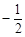 ,则椭圆离心率为
,则椭圆离心率为 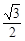
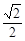
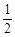
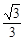
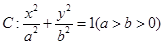 的离心率为
的离心率为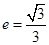 ,以原点为圆心,椭圆短半轴长为半径的圆与直线
,以原点为圆心,椭圆短半轴长为半径的圆与直线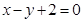 相切,
相切,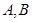 分别是椭圆的左右两个顶点,
分别是椭圆的左右两个顶点,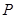 为椭圆
为椭圆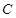 上的动点.
上的动点.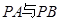 的斜率分别为
的斜率分别为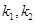 ,求
,求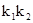 的值。
的值。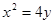 焦点的直线依次交抛物线与圆
焦点的直线依次交抛物线与圆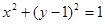 于点A、B、C、D,则
于点A、B、C、D,则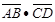 的值是( )
的值是( )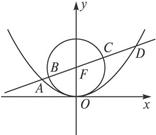
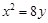 的准线方程是
的准线方程是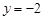
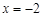
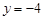
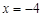
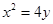 的准线方程为 .
的准线方程为 .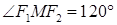 ,则双曲线离心率为
,则双曲线离心率为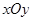 中,点
中,点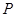 到两点
到两点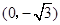 ,
,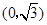 的距离之和等于
的距离之和等于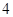 ,设点
,设点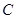 。
。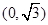 作两条互相垂直的直线
作两条互相垂直的直线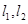 分别与曲线
分别与曲线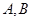 和
和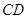 。
。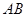 为直径的圆过能否过坐标原点,若能求出此时的
为直径的圆过能否过坐标原点,若能求出此时的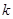 值,若不能说明理由;
值,若不能说明理由;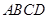 面积的取值范围。
面积的取值范围。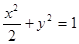 的右焦点作倾斜角为
的右焦点作倾斜角为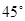 的直线
的直线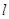 ,交椭圆于A、B两点,O为坐标原点,则
,交椭圆于A、B两点,O为坐标原点,则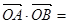 ( )
( )