题目内容
在等差数列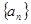 中,
中,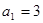 ,其前
,其前 项和为
项和为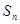 ,等比数列
,等比数列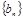 的各项均为正数,
的各项均为正数, ,公比为
,公比为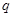 ,且
,且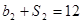 ,
,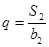 .
.
(1)求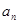 与
与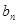 ; (2)设数列
; (2)设数列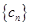 满足
满足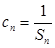 ,求
,求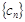 的前
的前 项和
项和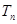 .
.
(1) ,
, ;(2)
;(2) 。
。
解析试题分析:(1)设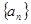 的公差为
的公差为 ,则
,则 ,然后代入
,然后代入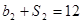 ,
,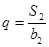
可得关于 的方程,解出
的方程,解出 即可得到
即可得到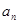 与
与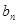 ;(2)由(1)可知
;(2)由(1)可知 ,
,
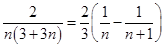 ,然后利用裂项相消求和,
,然后利用裂项相消求和,
试题解析:(1)设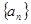 的公差为
的公差为 ,因为
,因为 所以
所以
解得  或
或 (舍),
(舍),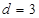 .故
.故 ,
, .
.
(2)由(1)可知 ,所以
,所以 .
.
故
考点:(1)等差(比)数列的通项公式;(2)裂项相消进行数列求和。

练习册系列答案
相关题目
 ,那么它的通项公式为an=_________
,那么它的通项公式为an=_________  的前
的前 项和为
项和为 且
且 .
. 的通项公式为
的通项公式为 ,问: 是否存在正整数t,使得
,问: 是否存在正整数t,使得
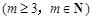 成等差数列?若存在,求出t和m的值;若不存在,请说明理由.
成等差数列?若存在,求出t和m的值;若不存在,请说明理由.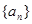 的前
的前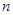 项和为
项和为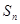 ,
,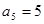 ,
,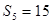 ,
,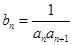 ,求数列
,求数列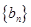 的前100项和.
的前100项和.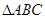 中,角
中,角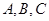 的对边分别为
的对边分别为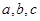 ,且
,且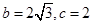 ,求
,求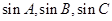 成等比数列,试判断
成等比数列,试判断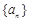 满足
满足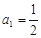 ,
,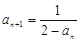
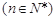 .
.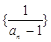 为等差数列,并求出
为等差数列,并求出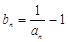 ,数列
,数列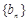 的前
的前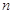 项和为
项和为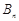 ,对任意
,对任意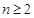 都有
都有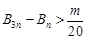 成立,求整数
成立,求整数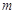 的最大值.
的最大值.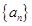 的前
的前 项和为
项和为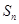 .若对任意的正整数
.若对任意的正整数 ,总存在正整数
,总存在正整数 ,使得
,使得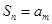 ,则称
,则称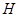 数列”.
数列”.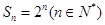 ,证明:
,证明: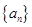 是等差数列,其首项
是等差数列,其首项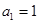 ,公差
,公差 ,若
,若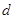 的值;
的值;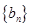 和
和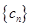 ,使得
,使得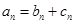
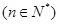 成立.
成立.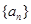 是等差数列,
是等差数列,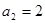 ,前四项和
,前四项和 。
。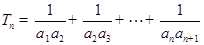 ,计算
,计算 。
。