题目内容
在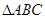 中,角
中,角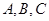 的对边分别为
的对边分别为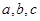 ,且
,且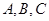 成等差数列
成等差数列
(1)若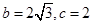 ,求
,求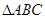 的面积
的面积
(2)若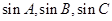 成等比数列,试判断
成等比数列,试判断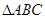 的形状
的形状
(1)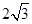 (2)等边三角形.
(2)等边三角形.
解析试题分析:(1)根据A、B、C成等差数列,结合A+B+C=π算出B= ,再由正弦定理得:
,再由正弦定理得: .根据b>c得C为锐角,得到C=
.根据b>c得C为锐角,得到C=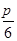 ,从而A=π-B-C=
,从而A=π-B-C=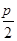 ,△ABC是直角三角形,由此不难求出它的面积.
,△ABC是直角三角形,由此不难求出它的面积.
(2)根据正弦定理,结合题意得b2=ac,根据B= ,利用余弦定理,得b2=a2+c2-ac,从而得到a2+c2-ac=ac,整理得得(a-c)2=0,由此即可得到△ABC为等边三角形.
,利用余弦定理,得b2=a2+c2-ac,从而得到a2+c2-ac=ac,整理得得(a-c)2=0,由此即可得到△ABC为等边三角形.
试题解析:∵A、B、C成等差数列,可得2B=A+C.
∴结合A+B+C=π,可得B= .
.
(1)∵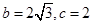 ,
,
∴由正弦定理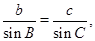 得
得 ,
,
∵b>c,可得B>C,∴C为锐角,得C=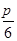 ,从而A=π-B-C=
,从而A=π-B-C=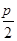 .
.
因此,△ABC的面积为S= bc=
bc= ×
×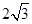 ×2=
×2=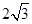 .
.
(2)∵sinA、sinB、sinC成等比数列,即sin2B=sinAsinC.
∴由正弦定理,得b2=ac
又∵根据余弦定理,得b2=a2+c2-2accosB=a2+c2-ac,
∴a2+c2-ac=ac,整理得(a-c)2=0,可得a=c
∵B= ,∴A=C=
,∴A=C= ,可得△ABC为等边三角形.
,可得△ABC为等边三角形.
考点:三角形内角和定理;利用正、余弦定理;三角形的形状判断,等差等比数列的性质.

练习册系列答案
相关题目
 的前n项和为
的前n项和为 ,且
,且
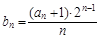 ,求数列
,求数列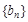 的前n项和Tn.
的前n项和Tn.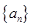 满足
满足 ,
,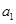 ,
,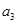 ,
,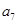 成等比数列.
成等比数列. 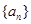 的通项公式;(2)数列
的通项公式;(2)数列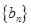 满足
满足 ,求数列
,求数列 项和
项和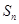 ;(Ⅲ)设
;(Ⅲ)设 ,若数列
,若数列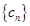 是单调递减数列,求实数
是单调递减数列,求实数 的取值范围.
的取值范围.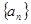 中,
中,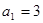 ,其前
,其前 项和为
项和为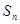 ,等比数列
,等比数列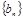 的各项均为正数,
的各项均为正数, ,公比为
,公比为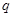 ,且
,且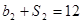 ,
,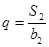 .
.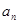 与
与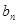 ; (2)设数列
; (2)设数列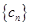 满足
满足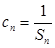 ,求
,求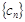 的前
的前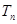 .
.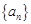 中,
中,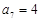 ,
,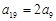 .
.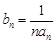 ,求数列
,求数列 的前
的前 项和
项和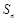 .
.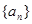 的前n项和为
的前n项和为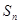 ,且
,且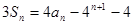
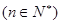 ,令
,令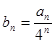 .
.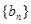 是等差数列,并求数列
是等差数列,并求数列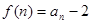
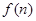 是18的倍数.
是18的倍数.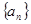 满足:
满足: ,
,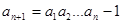 (
(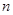 ≥3),记
≥3),记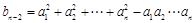
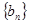 为等差数列,并求通项公式;
为等差数列,并求通项公式; ,数列{
,数列{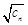 }的前n项和为
}的前n项和为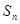 ,求证:
,求证: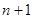 .
.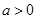 ,且
,且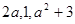 按某种顺序排列成等差数列.
按某种顺序排列成等差数列. 的值;
的值;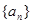 的首项和公差都为
的首项和公差都为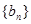 的首项和公比都为
的首项和公比都为 项和分别为
项和分别为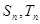 ,且
,且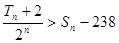 ,求满足条件的自然数
,求满足条件的自然数