题目内容
15.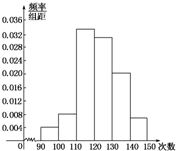 为了了解高一学生的体能情况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形面积之比为2:4:17:15:9:3,第二小组频数为12.
为了了解高一学生的体能情况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形面积之比为2:4:17:15:9:3,第二小组频数为12.(1)第二小组的频率是多少?样本容量是多少?
(2)规定次数在110以上(含110次)为达标,该校高一共有1050名学生,试估计该学校全体高一学生达标的人数有多少?
分析 (1)根据频率直方图得出从左到右的频率之比为2:4:17:15:9:3,得出第二小组的频率是P2=$\frac{4}{50}$=$\frac{2}{25}$,再利用$\frac{12}{n}$=$\frac{2}{25}$,可求解n,
(2)第-小组的频率是P1=$\frac{1}{2}$p2=$\frac{1}{25}$,第二小组的频率是P2=$\frac{2}{25}$,利用对立事件的频率求解达标的频率为:1-$\frac{1}{25}$-$\frac{2}{25}$=$\frac{22}{25}$,很容易估计该学校全体高一学生达标的人数1050×$\frac{22}{25}$.
解答 解:(1)根据题意得出:从左到右各小长方形面积之比为2:4:17:15:9:3,
∴从左到右的频率之比为2:4:17:15:9:3,
∵2+4+17+15+9+3=50
∴第二小组的频率是P2=$\frac{4}{50}$=$\frac{2}{25}$,
∵第二小组频数为12.
∴n=150,
(2)第-小组的频率是P1=$\frac{1}{2}$p2=$\frac{1}{25}$,
第二小组的频率是P2=$\frac{2}{25}$,
∴规定次数在110以上(含110次)为达标,达标的频率为:1-$\frac{1}{25}$-$\frac{2}{25}$=$\frac{22}{25}$,
∵该校高一共有1050名学生,
∴估计该学校全体高一学生达标的人数有:1050×$\frac{22}{25}$=924
点评 本题考察了运用频率直方图分析解决统计问题,关键是确定每段上的频率,对立事件的频率的关系,属于中档题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
6.已知△ABC中,∠A,∠B,∠C的对边分别为a,b,c,若a=1,2cosC+c=2b,则△ABC的周长的取值范围是( )
| A. | ($\frac{1}{2},2$] | B. | (1,3] | C. | (2,3] | D. | [3,5] |
10.甲、乙两人为了响应政府“节能减排”的号召,决定购置某品牌空调各一台.经了解,目前市场上销售此品牌空调有A,B,C三种型号,甲从A,B,C三类型号中挑选,乙从B,C两种型号中挑选,甲、乙二人选择各类车型的概率如下表:
若甲、乙都选C型号的概率为$\frac{3}{10}$.
(1)求p,q的值;
(2)某市对购买此品牌空调进行补贴,补贴标准如下表:
记甲、乙两人购空调所获得财政补贴的和为X,求X的分布列和期望.
 | A | B | C |
| 甲 | $\frac{1}{5}$ | p | q |
| 乙 |  | $\frac{1}{4}$ | $\frac{3}{4}$ |
(1)求p,q的值;
(2)某市对购买此品牌空调进行补贴,补贴标准如下表:
| 型号 | A | B | C |
| 补贴金额(百元/台) | 3 | 4 | 5 |
5.给出如下“三段论”推理:
因为整数是自然数,…大前提
而-5是整数,…小前提
所以-5是自然数.…结 论
则( )
因为整数是自然数,…大前提
而-5是整数,…小前提
所以-5是自然数.…结 论
则( )
| A. | 这个推理的形式错误 | B. | 这个推理的大前提错误 | ||
| C. | 这个推理的小前提错误 | D. | 这个推理正确 |