题目内容
(本小题满分12分)(注意:在试题卷上作答无效)
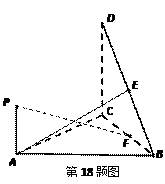
如图,直角△BCD所在的平面垂直于正△ABC所在的平面,
PA⊥平面ABC,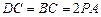 ,
,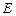 为DB的中点,
为DB的中点,
(Ⅰ)证明:AE⊥BC;
(Ⅱ)若点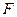 是线段
是线段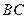 上的动点,设平面
上的动点,设平面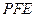 与平面
与平面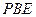 所成的平面角大小为
所成的平面角大小为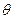 ,当
,当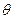 在
在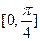 内取值时,求直线PF与平面DBC所成的角的范围。
内取值时,求直线PF与平面DBC所成的角的范围。
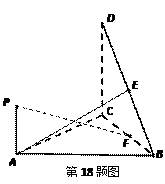
如图,直角△BCD所在的平面垂直于正△ABC所在的平面,
PA⊥平面ABC,
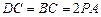 ,
,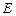 为DB的中点,
为DB的中点,(Ⅰ)证明:AE⊥BC;
(Ⅱ)若点
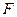 是线段
是线段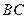 上的动点,设平面
上的动点,设平面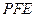 与平面
与平面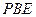 所成的平面角大小为
所成的平面角大小为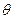 ,当
,当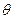 在
在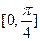 内取值时,求直线PF与平面DBC所成的角的范围。
内取值时,求直线PF与平面DBC所成的角的范围。(Ⅰ)AE⊥BC
(Ⅱ)直线PF与平面DBC所成的角的范围为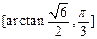
(Ⅱ)直线PF与平面DBC所成的角的范围为
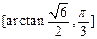
证明:(I)取BC的中点O,连接EO,AO, EO//DC所以EO⊥BC
因为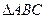 为等边三角形,所以BC⊥AO 所以BC⊥面AEO,故BC⊥AE ………4分
为等边三角形,所以BC⊥AO 所以BC⊥面AEO,故BC⊥AE ………4分
(II)连接PE,因为面BCD⊥面ABC,DC⊥BC,所以DC⊥面ABC,而EO
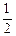 DC
DC
所以EO PA,故四边形APEO为矩形 ………………………………………5分
PA,故四边形APEO为矩形 ………………………………………5分
易证PE⊥面BCD,连接EF,则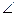 PFE为PF与面DBC所成的角, ………………7分
PFE为PF与面DBC所成的角, ………………7分
又PE⊥面BCD,所以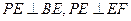 ,
,
∴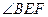 为面
为面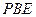 与面
与面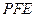 所成的角,即
所成的角,即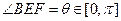 ,……………9分
,……………9分
此时点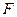 即在线段
即在线段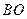 上移动,设
上移动,设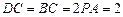 ,则
,则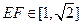 ,
,
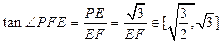 ,
,
所以直线PF与平面DBC所成的角的范围为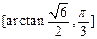 。…………………12分
。…………………12分
因为
 为等边三角形,所以BC⊥AO 所以BC⊥面AEO,故BC⊥AE ………4分
为等边三角形,所以BC⊥AO 所以BC⊥面AEO,故BC⊥AE ………4分(II)连接PE,因为面BCD⊥面ABC,DC⊥BC,所以DC⊥面ABC,而EO

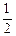 DC
DC所以EO
 PA,故四边形APEO为矩形 ………………………………………5分
PA,故四边形APEO为矩形 ………………………………………5分易证PE⊥面BCD,连接EF,则
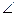 PFE为PF与面DBC所成的角, ………………7分
PFE为PF与面DBC所成的角, ………………7分又PE⊥面BCD,所以
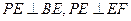 ,
,∴
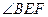 为面
为面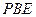 与面
与面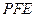 所成的角,即
所成的角,即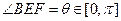 ,……………9分
,……………9分此时点
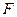 即在线段
即在线段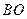 上移动,设
上移动,设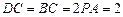 ,则
,则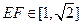 ,
,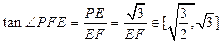 ,
,所以直线PF与平面DBC所成的角的范围为
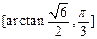 。…………………12分
。…………………12分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
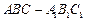 中,已知
中,已知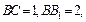
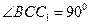 ,
,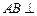 侧面
侧面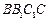
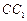 (不包含端点
(不包含端点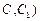 上确定一点
上确定一点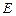 的位置,使得
的位置,使得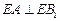 (要求说明理由).
(要求说明理由).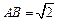 ,求二面角
,求二面角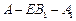 的大小.
的大小.
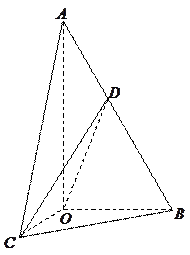
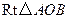 中,
中,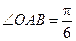 ,斜边
,斜边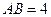 .
.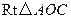 可以通过
可以通过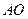 为轴旋转得到,且二面角
为轴旋转得到,且二面角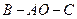 是直二面角.动点
是直二面角.动点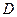 的斜边
的斜边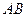 上.
上.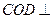 平面
平面 ;
;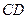 所成角的大小;
所成角的大小;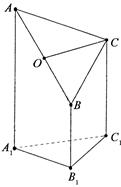
 .
. (2)在线段
(2)在线段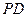 上是否存在一点
上是否存在一点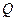 ,使
,使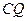 与平面
与平面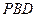 所成的角的正弦值为
所成的角的正弦值为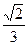 ,若存在,
,若存在, 中,
中,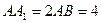 ,点
,点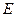 在
在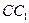 上且
上且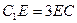 .
.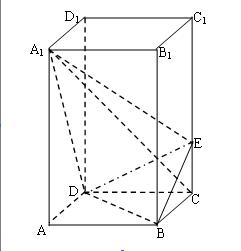
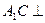 平面
平面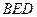 ;
;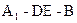 的余弦值.
的余弦值.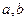 表示直线,
表示直线,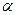 表示平面
表示平面 ,下列命题中正确的是( )
,下列命题中正确的是( )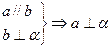
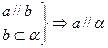
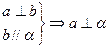

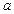 、
、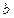 与直线
与直线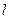 都成异面直线,则
都成异面直线,则