题目内容
11.在极坐标系中,已知A($\sqrt{2}$,0)到直线l:ρsin(θ-$\frac{π}{4}$)=m,(m>0)的距离为3.(1)求m的值.
(2)设P是直线l上的动点,点Q在线段OP上,满足|$\overrightarrow{OP}$|•|$\overrightarrow{OQ}$|=1,求点Q的轨迹方程.
分析 (1)以极点为原点,极轴为x的正半轴建立直角坐标系,求出A的坐标,直线l的直角坐标方程,利用点到直线的距离公式,即可求m的值.
(2)设Q(ρ,θ),P(ρ0,θ0),确定坐标之间的关系,即可求出点Q的轨迹方程.
解答 解:(1)以极点为原点,极轴为x的正半轴建立直角坐标系,则A($\sqrt{2}$,0),
直线l的直角坐标方程是:x-y-$\sqrt{2}m$=0,A到l的距离$d=\frac{{|{\sqrt{2}+\sqrt{2}m}|}}{{\sqrt{2}}}=3$
∴m=2…(7分)
(2)由(1)得直线l的极坐标方程为ρsin(θ-$\frac{π}{4}$)=2,设Q(ρ,θ),P(ρ0,θ0),
则$\left\{\begin{array}{l}ρ{ρ_0}=1\\ θ={θ_0}\end{array}\right.$,∴$\left\{\begin{array}{l}{ρ_0}=\frac{1}{ρ}\\{θ_0}=θ\end{array}\right.$
∵$P∈l∴{ρ_0}sin({θ_0}-\frac{π}{4})=2∴\frac{1}{ρ}sin(θ-\frac{π}{4})=2$
点Q的轨迹方程是:ρ=$\frac{1}{2}$sin(θ-$\frac{π}{4}$)…(14分)
点评 本题考查轨迹方程,考查极坐标方程,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
3.下列说法正确的是( )
| A. | 某人打靶,射击10次,击中7次,那么此人中靶的概率为0.7 | |
| B. | 一位同学做掷硬币试验,掷6次,一定有3次“正面朝上” | |
| C. | 某地发行福利彩票,回报率为47%,有人花了100元钱买彩票,一定会有47元的回报 | |
| D. | 概率等于1的事件不一定为必然事件 |
1.函数$y=\frac{ln(2x-1)}{{\sqrt{2-x}}}$的定义域为( )
| A. | ($\frac{1}{2}$,+∞) | B. | ($\frac{1}{2}$,2) | C. | ($\frac{1}{2}$,1) | D. | (-∞,2) |
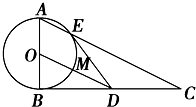 如图,△ABC是直角三角形,∠ABC=90°,以AB为直径的圆O交AC于点E,过E作圆的切线交BC于D点.连结OD交圆O于点M.
如图,△ABC是直角三角形,∠ABC=90°,以AB为直径的圆O交AC于点E,过E作圆的切线交BC于D点.连结OD交圆O于点M.