题目内容
(本题满分14分)
已知定义域为 的函数
的函数 是奇函数.
是奇函数.
(Ⅰ)求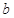 的值; (Ⅱ)判断函数
的值; (Ⅱ)判断函数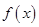 的单调性;
的单调性;
(Ⅲ)若对任意的 ,不等式
,不等式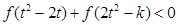 恒成立,求
恒成立,求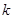 的取值范围.
的取值范围.
已知定义域为
 的函数
的函数 是奇函数.
是奇函数.(Ⅰ)求
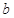 的值; (Ⅱ)判断函数
的值; (Ⅱ)判断函数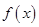 的单调性;
的单调性;(Ⅲ)若对任意的
 ,不等式
,不等式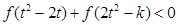 恒成立,求
恒成立,求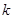 的取值范围.
的取值范围.(Ⅰ);(Ⅱ)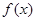 在
在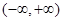 上为减函数. (Ⅲ)
上为减函数. (Ⅲ)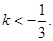
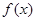 在
在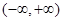 上为减函数. (Ⅲ)
上为减函数. (Ⅲ)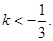
(I)可根据f(0)=0,建立关于b的方程,求出b的值.
(II)由(Ⅰ)知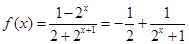 ,然后再利用单调性定义:第一步取值,作差并判断差值符号,下结论三个步取来判断.
,然后再利用单调性定义:第一步取值,作差并判断差值符号,下结论三个步取来判断.
(III)由(II)知f(x)在R上是增函数,所以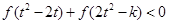 等价于
等价于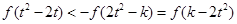 ,再利用单调性可转化为关于t的不等式
,再利用单调性可转化为关于t的不等式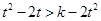 恒成立问题来解决.
恒成立问题来解决.
(Ⅰ)因为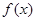 是奇函数,所以
是奇函数,所以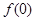 =0,
=0,
即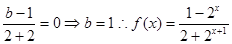 ………………………..3分
………………………..3分
(Ⅱ)由(Ⅰ)知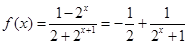 ,
,
设
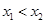 则
则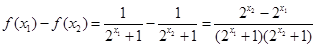
因为函数y=2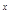 在R上是增函数且
在R上是增函数且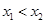 ∴
∴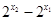 >0
>0
又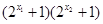 >0 ∴
>0 ∴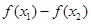 >0即
>0即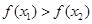
∴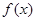 在
在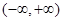 上为减函数. ……………7分
上为减函数. ……………7分
(Ⅲ)因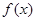 是奇函数,从而不等式:
是奇函数,从而不等式: 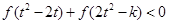
等价于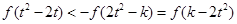 ,………….9分
,………….9分
因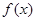 为减函数,由上式推得:
为减函数,由上式推得: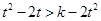 .即对一切
.即对一切 有:
有:
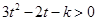 , ………………….12分
, ………………….12分
从而判别式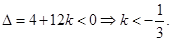 ……….14分
……….14分
(II)由(Ⅰ)知
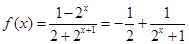 ,然后再利用单调性定义:第一步取值,作差并判断差值符号,下结论三个步取来判断.
,然后再利用单调性定义:第一步取值,作差并判断差值符号,下结论三个步取来判断.(III)由(II)知f(x)在R上是增函数,所以
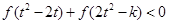 等价于
等价于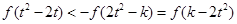 ,再利用单调性可转化为关于t的不等式
,再利用单调性可转化为关于t的不等式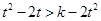 恒成立问题来解决.
恒成立问题来解决.(Ⅰ)因为
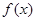 是奇函数,所以
是奇函数,所以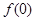 =0,
=0,即
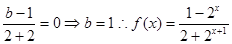 ………………………..3分
………………………..3分(Ⅱ)由(Ⅰ)知
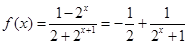 ,
,设

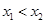 则
则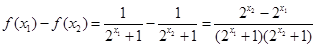
因为函数y=2
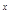 在R上是增函数且
在R上是增函数且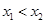 ∴
∴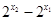 >0
>0又
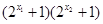 >0 ∴
>0 ∴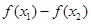 >0即
>0即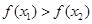
∴
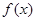 在
在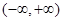 上为减函数. ……………7分
上为减函数. ……………7分(Ⅲ)因
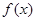 是奇函数,从而不等式:
是奇函数,从而不等式: 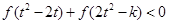
等价于
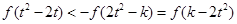 ,………….9分
,………….9分因
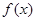 为减函数,由上式推得:
为减函数,由上式推得: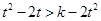 .即对一切
.即对一切 有:
有: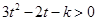 , ………………….12分
, ………………….12分从而判别式
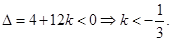 ……….14分
……….14分
练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
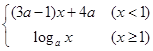 在区间
在区间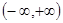 内是减函数,则
内是减函数,则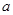 的取值范围是_______.
的取值范围是_______. 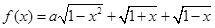 的最大值为
的最大值为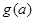 .
.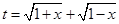 ,求
,求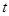 的取值范围;
的取值范围;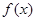 是定义在
是定义在 上的偶函数,当
上的偶函数,当 时,
时,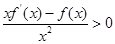 ,且
,且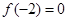 ,则不等式
,则不等式 的解集是( )
的解集是( )  ∪
∪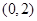
 ∪
∪
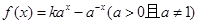 是定义域为R的奇函数.
是定义域为R的奇函数.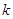 的值;
的值;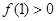 ,试判断函数单调性(不需证明)并求不等式
,试判断函数单调性(不需证明)并求不等式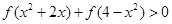 的解集;
的解集;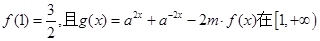 上的最小值为
上的最小值为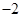 ,求
,求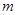 的值.
的值. 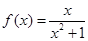 ,
,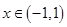 (1)判断此函数的奇偶性;(2)判断函数的单调性,并加以证明.(3)解不等式
(1)判断此函数的奇偶性;(2)判断函数的单调性,并加以证明.(3)解不等式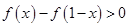
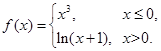 若
若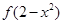 >
>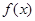 ,则实数
,则实数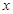 的取值范围是
的取值范围是
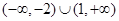


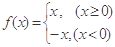 ,则
,则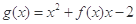 的单调递增区间为( )
的单调递增区间为( )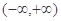
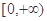
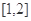
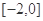
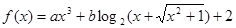 在
在 上有最小值-5,(
上有最小值-5,( ,
, 为常数),则函数
为常数),则函数 在
在 上( )
上( )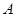 .有最大值5
.有最大值5  .有最小值5
.有最小值5  .有最大值3
.有最大值3  .有最大值9
.有最大值9