题目内容
已知等比数列{an},若a1+a2+a3=7,a1a2a3=8,求an.
∵a1a3=a22,∴a1a2a3=a23=8.∴a2=2.
从而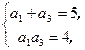 解得
解得 或
或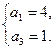
当a1=1时,q=2;当a1=4时,q= .
.
故an=2n-1或an=23-n.
从而
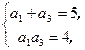 解得
解得 或
或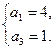
当a1=1时,q=2;当a1=4时,q=
 .
.故an=2n-1或an=23-n.
求等比数列的通项公式,只要求出a1和q即可.由于a1,a2,a3成等比数列,∴
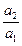 =
= ,即a22=a1a3.由此可求a2,再由条件即可解得a1和q;或利用a2=a1q,a3=a1q2将已知关系化简为a1和q的方程求解;或将a1=
,即a22=a1a3.由此可求a2,再由条件即可解得a1和q;或利用a2=a1q,a3=a1q2将已知关系化简为a1和q的方程求解;或将a1= ,a3=a2q代入已知条件进行求解.
,a3=a2q代入已知条件进行求解.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
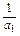 +
+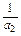 +
+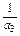 +
+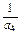 +
+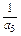 =2,求a3.
=2,求a3.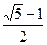 <r<
<r<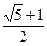 B.0<r<
B.0<r<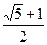
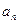 }的公比
}的公比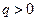 ,已知
,已知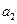 =1,
=1,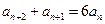 ,则{
,则{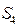 = 。
= 。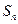 为等比数列
为等比数列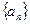 的前
的前 项和,
项和,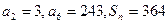 ,则
,则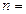 ;
;