题目内容
已知数列{an}的前n项和Sn=2an+1,求证:数列{an}是等比数列,并求出通项公式.
证明:∵Sn=2an+1,∴Sn+1=2an+1+1.
∴Sn+1-Sn=(2an+1+1)-(2an+1)=2an+1-2an.
∴an+1=2an. ①
又∵S1=a1=2a1+1,∴a1=-1≠0.
由①知,an≠0,
∴由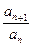 =2知,数列{an}是等比数列,an=-2n-1.
=2知,数列{an}是等比数列,an=-2n-1.
∴Sn+1-Sn=(2an+1+1)-(2an+1)=2an+1-2an.
∴an+1=2an. ①
又∵S1=a1=2a1+1,∴a1=-1≠0.
由①知,an≠0,
∴由
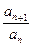 =2知,数列{an}是等比数列,an=-2n-1.
=2知,数列{an}是等比数列,an=-2n-1.要证数列是等比数列,关键是看an与an-1之比是否为一常数,由题设还需利用an=Sn-Sn-1(n≥2)求得an.
(1)本题证明,关键是用等比数列的定义,其中说明an≠0是非常重要的.证明中,也可以写出Sn-1=2an-1+1,从而得到an=2an-1,只能得到n≥2时,{an}是等比数列,得到n≥2时,an=-2n-1,再将n=1时,a1=-1代入验证.
(2)证明一个数列是等比数列,常用方法是:①要证明一个数列{an}是等比数列,只要证明对于任意自然数n,
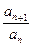 都等于同一个常数即可.②对于一个数列,除了首项和末项(有穷数列)外,任何一项都是它的前后两项的等比中项,则此数列是等比数列.
都等于同一个常数即可.②对于一个数列,除了首项和末项(有穷数列)外,任何一项都是它的前后两项的等比中项,则此数列是等比数列.
练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
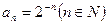 ,从数列
,从数列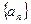 中取出部分项,按原来的顺序组成一个各项和为
中取出部分项,按原来的顺序组成一个各项和为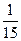 的无穷等比数列
的无穷等比数列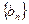 ,则
,则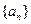 是等比数列,且
是等比数列,且 ,
, ,则
,则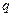 为
为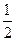
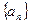 中,
中,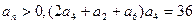 ,则
,则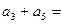 .
.