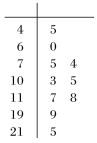
题目内容
【题目】如图,已知椭圆C:![]() +y2=1(a>1)的上顶点为A,右焦点为F,直线AF与圆M:x2+y2-6x-2y+7=0相切.
+y2=1(a>1)的上顶点为A,右焦点为F,直线AF与圆M:x2+y2-6x-2y+7=0相切.
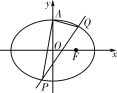
(1)求椭圆C的方程;
(2)若不过点A的动直线l与椭圆C相交于P,Q两点,且![]() =0,求证:直线l过定点,并求出该定点N的坐标.
=0,求证:直线l过定点,并求出该定点N的坐标.
【答案】(1)![]() +y2=1(2)证明见解析,定点N
+y2=1(2)证明见解析,定点N![]() .
.
【解析】
(1)利用直线AF与圆相切可求得a(圆心到直线的距离等于半径),从而得椭圆方程;
(2)由![]() =0,知AP⊥AQ,从而直线AP与坐标轴不垂直,设直线AP的方程为y=kx+1,代入椭圆方程可求得P点坐标,同理可得Q点坐标,写出直线PQ方程,化简后可知其所过定点.
=0,知AP⊥AQ,从而直线AP与坐标轴不垂直,设直线AP的方程为y=kx+1,代入椭圆方程可求得P点坐标,同理可得Q点坐标,写出直线PQ方程,化简后可知其所过定点.
(1)将圆M的一般方程x2+y2-6x-2y+7=0化为标准方程为(x-3)2+(y-1)2=3,圆M的圆心为M(3,1),半径为r=![]() .
.
由A(0,1),F(c,0)(c=![]() )得直线AF:
)得直线AF:![]() +y=1,即x+cy-c=0.
+y=1,即x+cy-c=0.
由直线AF与圆M相切得![]() =
=![]() .
.
所以c=![]() 或c=-
或c=-![]() (舍去).所以a=
(舍去).所以a=![]() ,
,
所以椭圆C的方程为![]() +y2=1.
+y2=1.
(2)证明:由![]() =0,知AP⊥AQ,从而直线AP与坐标轴不垂直,
=0,知AP⊥AQ,从而直线AP与坐标轴不垂直,
由A(0,1)可设直线AP的方程为y=kx+1,直线AQ的方程为y=-![]() x+1(k≠0),
x+1(k≠0),
将y=kx+1代入椭圆C的方程![]() +y2=1并整理,得(1+3k2)x2+6kx=0,
+y2=1并整理,得(1+3k2)x2+6kx=0,
解得x=0或x=-![]() ,
,
因此P的坐标为 ,即
,即 .
.
将上式中的k换成-![]() ,得Q
,得Q .
.
所以直线l的方程为y= ·
·![]() +
+![]() ,
,
化简得直线l的方程为y=![]() x-
x-![]() .
.
因此直线l过定点N![]() .
.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目