题目内容
【题目】给定一个四面体，若存在一个侧面(其所在平面为
)，使得在将其余三个侧面分别绕其位于平面上的边向体外方向旋转至平面上时，四个侧面在平面上共同组成的图形恰好是一个三角形，则称该四面体是一个“平展四面体”．若有一个平展四面体，它的一个侧面的三边长为a、b、c，试确定a、b、c的关系，并求该四面体的体积(用a、b、c表示)．
【答案】
【解析】
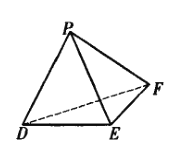
如图，若四面体PDEF为平展四面体，且沿
所在平面展平后的三角形为
，则DE、EF、FD为的中位线．被其三条中位线所划分成的四个全等三角形构成四面体的四个侧面，从而，四面体中共顶点的三个面角恰等于的三个内角．故为锐角三角形，且三边长为2a、2b、2c．
不妨设
,
.
则由为锐角三角形知
.
下面计算四面体PDEF的体积V.
设的外接圆半径为R，
.
则
.
设二面角P—DE—F的平面角为
．则
.
故
注意到
,
且
，则
练习册系列答案
相关题目
