题目内容
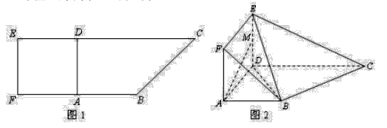
【题目】如图 1,在直角梯形![]() 中,
中, ![]() ,且
,且![]() .现以
.现以![]() 为一边向外作正方形
为一边向外作正方形![]() ,然后沿边
,然后沿边![]() 将正方形
将正方形![]() 翻折,使
翻折,使![]() 平面与平面
平面与平面![]() 垂直,
垂直, ![]() 为
为![]() 的中点,如图 2.
的中点,如图 2.
(1)求证: ![]() 平面
平面![]() ;
;
(2)求证: ![]() 平面
平面![]() ;
;
(3)求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】试题分析:
(1)取EC中点N,连结MN,BN.由几何关系可证得四边形ABNM为平行四边形.则BN∥AM,利用线面平行的判定定理可得![]() 平面
平面![]() ;
;
(2) 由几何关系有ED⊥AD,利用面面垂直的性质定理可得ED⊥平面ABCD,则ED⊥BC,利用直角梯形的性质结合勾股定理可得BC⊥BD,据此由线面垂直的判定定理有![]() 平面
平面![]() ;
;
(3) 作![]() 平面PEC于点H,连接CH,则∠DCH为所求的角,利用三棱锥体积相等转化顶点有:
平面PEC于点H,连接CH,则∠DCH为所求的角,利用三棱锥体积相等转化顶点有: ![]() ,据此可求得
,据此可求得![]() ,利用三角函数的定义可得
,利用三角函数的定义可得![]() 与平面
与平面![]() 所成角的正弦值是
所成角的正弦值是![]() .
.
试题解析:
(1)证明:取![]() 中点
中点![]() ,连结
,连结![]() .
.
在![]() 中,
中, ![]() 分别为
分别为![]() 的中点,
的中点,
所以![]() ,且
,且![]() .
.
由已知![]() ,
,
所以四边形![]() 为平行四边形.
为平行四边形.
所以![]() .
.
又因为![]() 平面
平面![]() ,且
,且![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(2)证明:在正方形![]() 中,
中, ![]() ,
,
又因为平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
所以![]()
在直角梯形![]() 中,
中, ![]() ,可得
,可得![]() .
.
在![]() 中,
中, ![]() .
.
所以![]() .
.
所以![]() 平面
平面![]() .
.
(3)作![]() 于点
于点![]() ,连接
,连接![]() ,则
,则![]() 为所求的角
为所求的角
由(2)知, ![]()
所以![]() ,又因为
,又因为![]() 平面
平面![]()
又![]() .
.
所以, ![]()
 .
.

【题目】甲、乙两个班级(各40名学生)进行一门考试,为易于统计分析,将甲、乙两个班学生的成绩分成如下四组:![]() ,
,![]() ,
,![]() ,
,![]() ,并分别绘制了如下的频率分布直方图:
,并分别绘制了如下的频率分布直方图:
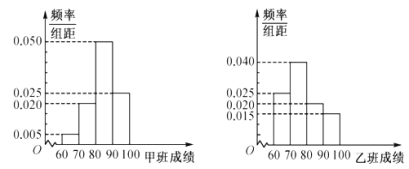
规定:成绩不低于90分的为优秀,低于90分的为不优秀.
(1)根据这次抽查的数据,填写下面的![]() 列联表:
列联表:
优秀 | 不优秀 | 合计 | |
甲班 | |||
乙班 | |||
合计 |
(2)根据(1)中的列联表,能否有![]() 的把握认为成绩是否优秀与班级有关?
的把握认为成绩是否优秀与班级有关?
附:临界值参考表与参考公式
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(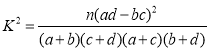 ,其中
,其中![]() )
)