题目内容
【题目】假设每天从甲地去乙地的旅客人数X是服从正态分布N(800,502)的随机变量.记一天中从甲地去乙地的旅客人数不超过900的概率为p0 .
(1)求p0的值;
(参考数据:若X~N(μ,σ2),有P(μ﹣σ<X≤μ+σ)=0.6826,P(μ﹣2σ<X≤μ+2σ)=0.9544,P(μ﹣3σ<X≤μ+3σ)=0.9974.)
(2)某客运公司用A,B两种型号的车辆承担甲、乙两地间的长途客运业务,每车每天往返一次,A,B两种车辆的载客量分别为36人和60人,从甲地去乙地的营运成本分别为1600元/辆和2400元/辆.公司拟组建一个不超过21辆车的客运车队,并要求B型车不多于A型车7辆.若每天要以不小于p0的概率运完从甲地去乙地的旅客,且使公司从甲地去乙地的营运成本最小,那么应配备A型车、B型车各多少辆?
【答案】
(1)解:由于随机变量X服从正态分布N(800,502),故有μ=800,σ=50,P(700<X≤900)=0.9544.
由正态分布的对称性,可得p0=(P(X≤900)=P(X≤800)+P(800<X≤900)= ![]()
(2)解:设A型、B型车辆的数量分别为x,y辆,则相应的营运成本为1600x+2400y.
依题意,x,y还需满足:x+y≤21,y≤x+7,P(X≤36x+60y)≥p0.
由(1)知,p0=P(X≤900),故P(X≤36x+60y)≥p0等价于36x+60y≥900.
于是问题等价于求满足约束条件 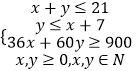
且使目标函数z=1600x+2400y达到最小值的x,y.
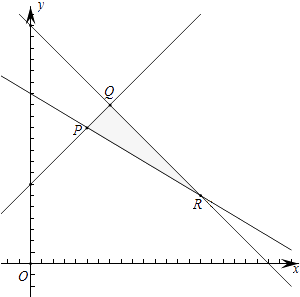
作可行域如图所示,可行域的三个顶点坐标分别为P(5,12),Q(7,14),R(15,6).
由图可知,当直线z=1600x+2400y经过可行域的点P时,直线z=1600x+2400y在y轴上截距 ![]() 最小,即z取得最小值.
最小,即z取得最小值.
故应配备A型车5辆,B型车12辆.
【解析】(1)变量服从正态分布N(800,502),即服从均值为800,标准差为50的正态分布,适合700<X≤900范围内取值即在(μ﹣2σ,μ+2σ)内取值,其概率为:95.44%,从而由正态分布的对称性得出不超过900的概率为p0 . (2)设每天应派出A型x辆、B型车y辆,根据条件列出不等式组,即得线性约束条件,列出目标函数,画出可行域求解.

【题目】某餐厅通过查阅了最近5次食品交易会参会人数![]() (万人)与餐厅所用原材料数量
(万人)与餐厅所用原材料数量![]() (袋),得到如下统计表:
(袋),得到如下统计表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
参会人数 | 13 | 9 | 8 | 10 | 12 |
原材料 | 32 | 23 | 18 | 24 | 28 |
(1)根据所给5组数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() .
.
(2)已知购买原材料的费用![]() (元)与数量
(元)与数量![]() (袋)的关系为
(袋)的关系为![]() ,
,
投入使用的每袋原材料相应的销售收入为700元,多余的原材料只能无偿返还,据悉本次交易大会大约有15万人参加,根据(1)中求出的线性回归方程,预测餐厅应购买多少袋原材料,才能获得最大利润,最大利润是多少?(注:利润![]() 销售收入
销售收入![]() 原材料费用).
原材料费用).
参考公式:  ,
, ![]() .
.
参考数据: ![]() ,
, ![]() ,
, ![]() .
.
【题目】设二次函数f(x)=ax2+bx.
(1)若1≤f(-1)≤2,2≤f(1)≤4,求f(-2)的取值范围;
(2)当b=1时,若对任意x∈[0,1],-1≤f(x)≤1恒成立,求实数a的取值范围.
【题目】某个产品有若千零部件构成,加工时需要经过6道工序,分别记为![]() .其中,有些工序因为是制造不同的零部件,所以可以在几台机器上同时加工;有些工序因为是对同一个零部件进行处理,所以存在加工顺序关系.若加工工序
.其中,有些工序因为是制造不同的零部件,所以可以在几台机器上同时加工;有些工序因为是对同一个零部件进行处理,所以存在加工顺序关系.若加工工序![]() 必须要在工序
必须要在工序![]() 完成后才能开工,则称
完成后才能开工,则称![]() 为
为![]() 的紧前工序.现将各工序的加工次序及所需时间(单位:小时)列表如下:
的紧前工序.现将各工序的加工次序及所需时间(单位:小时)列表如下:
工序 |
|
|
|
|
|
|
加工时间 | 3 | 4 | 2 | 2 | 2 | 1 |
紧前工序 | 无 |
| 无 |
|
|
|
现有两台性能相同的生产机器同时加工该产品,则完成该产品的最短加工时间是__________小时.(假定每道工序只能安排在一台机器上,且不能间断).


