Question

【题目】已知a＞0，函数 ．
（1）记f（x）在区间[0，4]上的最大值为g（a），求g（a）的表达式；
（2）是否存在a使函数y=f（x）在区间（0，4）内的图象上存在两点，在该两点处的切线互相垂直？若存在，求出a的取值范围；若不存在，请说明理由．

Answer 1

【答案】
（1）解：当0≤x≤a时， ；当x＞a时，

∴当0≤x≤a时， ，f（x）在（0，a）上单调递减；

当x＞a时， ，f（x）在（a，+∞）上单调递增．

①若a≥4，则f（x）在（0，4）上单调递减，g（a）=f（0）=

②若0＜a＜4，则f（x）在（0，a）上单调递减，在（a，4）上单调递增

∴g（a）=max{f（0），f（4）}

∵f（0）﹣f（4）= =

∴当0＜a≤1时，g（a）=f（4）= ；当1＜a＜4时，g（a）=f（0）= ，

综上所述，g（a）= ；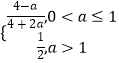

（2）解：由（1）知，当a≥4时，f（x）在（0，4）上单调递减，故不满足要求；

当0＜a＜4时，f（x）在（0，a）上单调递减，在（a，4）上单调递增，若存在x1，x2∈（0，4）（x1＜x2），使曲线y=f（x）在

两点处的切线互相垂直，则x1∈（0，a），x2∈（a，4），且f′（x1）f′（x2）=﹣1

∴ =﹣1

∴ ①

∵x1∈（0，a），x2∈（a，4），

∴x1+2a∈（2a，3a）， ∈（ ，1）

∴①成立等价于A=（2a，3a）与B=（ ，1）的交集非空

∵ ，∴当且仅当0＜2a＜1，即 时，A∩B≠

综上所述，存在a使函数y=f（x）在区间（0，4）内的图象上存在两点，在该两点处的切线互相垂直，且a的取值范围是（0， ）．

【解析】（1）利用绝对值的几何意义，分类讨论，结合导数确定函数的单调性，从而可得g（a）的表达式；（2）利用曲线y=f（x）在两点处的切线互相垂直，建立方程，从而可转化为集合的运算，即可求得结论．
【考点精析】解答此题的关键在于理解函数的最大(小)值与导数的相关知识，掌握求函数在上的最大值与最小值的步骤：（1）求函数在内的极值；（2）将函数的各极值与端点处的函数值，比较，其中最大的是一个最大值，最小的是最小值．