题目内容
【题目】在平面直角坐标系xOy中，C1的参数方程为
(t为参数)，在以坐标原点为极点，x轴正半轴为极轴的极坐标系中，C2的极坐标方程ρ2－2ρcos θ－3＝0.
(Ⅰ)说明C2是哪种曲线，并将C2的方程化为普通方程；
(Ⅱ)C1与C2有两个公共点A，B，定点P的极坐标
，求线段AB的长及定点P到A，B两点的距离之积．
【答案】(Ⅰ)C2是圆，C2的普通方程是：(x－1)2＋y2＝4.(Ⅱ)答案见解析.
【解析】试题分析：（1）C2是圆，利用极坐标方程与普通方程转化方法，将C2的方程化为普通方程；（2）利用参数的几何意义，求线段AB的长及定点P到A，B两点的距离之积．
试题解析：
(Ⅰ)C2是圆，C2的极坐标方程ρ2－2ρcos θ－3＝0，
化为普通方程：x2＋y2－2x－3＝0即：(x－1)2＋y2＝4.
(Ⅱ)P的极坐标为
，
平面直角坐标为(1,1)，在直线C1上，
将C1的参数方程为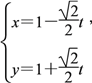
(t为参数)
代入x2＋y2－2x－3＝0中得：
2＋
2－2－3＝0
化简得：t2＋
t－3＝0 设两根分别为t1，t2，
由韦达定理知：
所以AB的长|AB|＝|t1－t2|
＝
＝
＝
，
定点P到A，B两点的距离之积
|PA|·|PB|＝|t1t2|＝3.
练习册系列答案
相关题目
【题目】已知函数f(x)＝
sinωxcosωx－cos2ωx＋
(ω＞0)，经化简后利用“五点法”画其在某一周期内的图象时，列表并填入的部分数据如下表：
x | ① |
|
| ||
f(x) | 0 | 1 | 0 | －1 | 0 |
(1)请直接写出①处应填的值，并求函数f(x)在区间
上的值域；
(2)△ABC的内角A，B，C所对的边分别为a，b，c，已知f(A＋
)＝1，b＋c＝4，a＝
，求△ABC的面积．
