[题目]如图.直三棱柱中.分别是的中点..(1)证明:平面,(2)求二面角的余弦值. 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图，直三棱柱中，分别是的中点，.

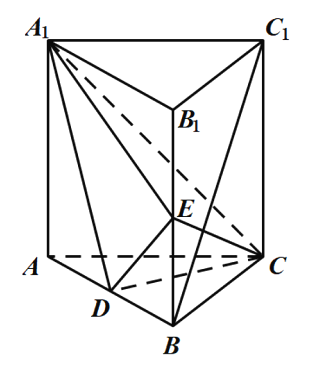
（1）证明：平面；

（2）求二面角的余弦值.

【答案】(1)证明见解析 (2)

【解析】

（1）连接交于点，由三角形中位线定理得，由此能证明平面．

（2）以为坐标原点，的方向为轴正方向，的方向为轴正方向，的方向为轴正方向，建立空间直角坐标系．分别求出平面的法向量和平面的法向量，利用向量法能求出二面角的余弦值．

证明：证明：连接交于点，

则为的中点．又是的中点，

连接，则．

因为平面，平面，

所以平面．

（2）由，可得：，即

所以

又因为直棱柱，所以以点为坐标原点，分别以直线为轴、轴、轴，建立空间直角坐标系，则，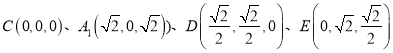

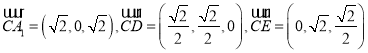
设平面的法向量为，则且，可解得，令，得平面的一个法向量为，

同理可得平面的一个法向量为，

则

所以二面角的余弦值为.

练习册系列答案

相关题目

【题目】已知数列,满足（…）．

（1）若，求的值；

（2）若且，则数列中第几项最小？请说明理由；

（3）若（n=1,2,3,…），求证：“数列为等差数列”的充分必要条件是“数列为等差数列且（n=1,2,3,…）”．

【题目】已知椭圆的离心率为，且与双曲线有相同的焦点.

（1）求椭圆的方程；

（2）直线与椭圆相交于，两点，点满足，点，若直线斜率为，求面积的最大值及此时直线的方程.

【题目】设函数为常数) .

(1)当时，求曲线在处的切线方程:

(2)若函数在内存在唯一极值点，求实数的取值范围，并判断，是在内的极大值点还是极小值点.

【题目】已知椭圆：的两个焦点与短轴的一个端点是直角三角形的三个顶点，直线：与椭圆有且只有一个公共点．

（Ⅰ）求椭圆的方程及点的坐标；

（Ⅱ）设是坐标原点，直线平行于，与椭圆交于不同的两点、，且与直线交于点，证明：存在常数，使得，并求的值．

【题目】已知椭圆C：（）的焦距为4，其短轴的两个端点与长轴的一个端点构成正三角形.

（1）求椭圆C的标准方程；

（2）设F为椭圆C的左焦点，T为直线上任意一点，过F作TF的垂线交椭圆C于点P，Q.

（i）证明：OT平分线段PQ（其中O为坐标原点）；

（ii）当最小时，求点T的坐标.

【题目】如图，已知椭圆过点两个焦点为和.圆O的方程为.

（1）求椭圆C的标准方程；

（2）过且斜率为的动直线l与椭圆C交于A、B两点，与圆O交于P、Q两点（点A、P在x轴上方），当成等差数列时，求弦PQ的长.

【题目】大数据时代对于现代人的数据分析能力要求越来越高，数据拟合是一种把现有数据通过数学方法来代入某条数式的表示方式，比如，，2，，n是平面直角坐标系上的一系列点，用函数来拟合该组数据，尽可能使得函数图象与点列比较接近．其中一种描述接近程度的指标是函数的拟合误差，拟合误差越小越好，定义函数的拟合误差为：．已知平面直角坐标系上5个点的坐标数据如表：