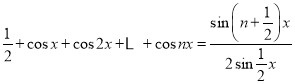题目内容
【题目】已知椭圆C:![]() (
(![]() )的焦距为4,其短轴的两个端点与长轴的一个端点构成正三角形.
)的焦距为4,其短轴的两个端点与长轴的一个端点构成正三角形.
(1)求椭圆C的标准方程;
(2)设F为椭圆C的左焦点,T为直线![]() 上任意一点,过F作TF的垂线交椭圆C于点P,Q.
上任意一点,过F作TF的垂线交椭圆C于点P,Q.
(i)证明:OT平分线段PQ(其中O为坐标原点);
(ii)当![]() 最小时,求点T的坐标.
最小时,求点T的坐标.
【答案】(1)![]() ;(2)证明见解析,
;(2)证明见解析,![]()
【解析】
(1)由题意![]() ,又
,又![]() ,由此可求出
,由此可求出![]() 的值,从而求得椭圆的方程.(2)椭圆方程化为
的值,从而求得椭圆的方程.(2)椭圆方程化为![]() .设PQ的方程为
.设PQ的方程为![]() ,代入椭圆方程得:
,代入椭圆方程得:![]() .(ⅰ)设PQ的中点为
.(ⅰ)设PQ的中点为![]() ,求出
,求出![]() ,只要
,只要![]() ,即证得OT平分线段PQ.(ⅱ)可用
,即证得OT平分线段PQ.(ⅱ)可用![]() 表示出PQ,TF可得:
表示出PQ,TF可得:![]() 化简得:
化简得: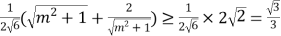 .再根据取等号的条件,可得T的坐标.
.再根据取等号的条件,可得T的坐标.
(1)![]() ,又
,又![]() .
.
(2)椭圆方程化为![]() .
.
(ⅰ)设PQ的方程为![]() ,代入椭圆方程得:
,代入椭圆方程得:![]() .
.
设PQ的中点为![]() ,则
,则![]()
又TF的方程为![]() ,则
,则![]() 得
得![]() ,
,
所以![]() ,即OT过PQ的中点,即OT平分线段PQ.
,即OT过PQ的中点,即OT平分线段PQ.
(ⅱ)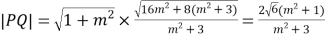 ,又
,又![]() ,所以
,所以
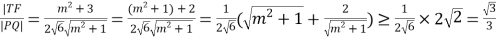 .
.
当![]() 时取等号,此时T的坐标为
时取等号,此时T的坐标为![]() .
.

练习册系列答案
相关题目
【题目】某校举行了全体学生的一分钟跳绳比赛,为了了解学生的体质,随机抽取了100名学生,其跳绳个数的频数分布表如下:
一分钟跳绳个数 |
|
|
|
|
|
|
|
频数 | 6 | 12 | 18 | 30 | 16 | 10 | 8 |
(1)若将抽取的100名学生一分钟跳绳个数作为一个样本,请将这100名学生一分钟跳绳个数的频率分布直方图补充完整(只画图,不需要写出计算过程);
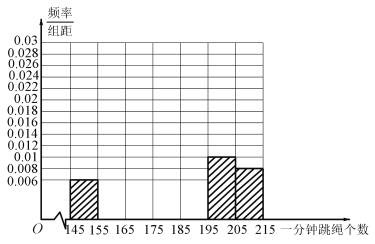
(2)若该校共有3000名学生,所有学生的一分钟跳绳个数X近似服从正态分布![]() ,其中
,其中![]() 为样本平均数的估计值(同一组中的数据用该组区间的中点值为代表).利用所得正态分布模型,解决以下问题:
为样本平均数的估计值(同一组中的数据用该组区间的中点值为代表).利用所得正态分布模型,解决以下问题:
①估计该校一分钟跳绳个数超过165个的人数(结果四舍五入到整数);
②若在该校所有学生中任意抽取4人,设一分钟跳绳个数超过180个的人数为![]() ,求随机变量
,求随机变量![]() 的分布列、期望与方差./span>
的分布列、期望与方差./span>
附:若随机变量Z服从正态分布![]() ,则
,则![]() ,
,![]() ,
,![]() .
.