题目内容
【题目】已知椭圆![]() :
: ![]() 的两个焦点与短轴的一个端点是直角三角形的三个顶点,直线
的两个焦点与短轴的一个端点是直角三角形的三个顶点,直线![]() :
: ![]() 与椭圆
与椭圆![]() 有且只有一个公共点.
有且只有一个公共点.
(Ⅰ)求椭圆![]() 的方程及点
的方程及点![]() 的坐标;
的坐标;
(Ⅱ)设![]() 是坐标原点,直线
是坐标原点,直线![]() 平行于
平行于![]() ,与椭圆
,与椭圆![]() 交于不同的两点
交于不同的两点![]() 、
、![]() ,且与直线
,且与直线![]() 交于点
交于点![]() ,证明:存在常数
,证明:存在常数![]() ,使得
,使得![]() ,并求
,并求![]() 的值.
的值.
【答案】(Ⅰ)![]() ,点T坐标为(2,1);(Ⅱ)
,点T坐标为(2,1);(Ⅱ)![]() .
.
【解析】试题分析:本题考查椭圆的标准方程及其几何性质,考查学生的分析问题、解决问题的能力和数形结合的思想.第(Ⅰ)问,利用直线和椭圆只有一个公共点,联立方程,消去y得关于x的方程有两个相等的实数根,解出b的值,从而得到椭圆E的方程;第(Ⅱ)问,利用椭圆的几何性质,数形结合,根据根与系数的关系,进行求解.
试题解析:(Ⅰ)由已知, ![]() ,则椭圆E的方程为
,则椭圆E的方程为![]() .
.
由方程组 得
得![]() .①
.①
方程①的判别式为![]() ,由
,由![]() ,得
,得![]() ,
,
此时方程①的解为![]() ,
,
所以椭圆E的方程为![]() .
.
点T坐标为(2,1).
(Ⅱ)由已知可设直线![]() 的方程为
的方程为![]() ,
,
由方程组 可得
可得
所以P点坐标为(![]() ),
),![]() .
.
设点A,B的坐标分别为![]() .
.
由方程组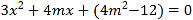 可得
可得![]() .②
.②
方程②的判别式为![]() ,由
,由![]() ,解得
,解得![]() .
.
由②得![]() .
.
所以 ,
,
同理![]() ,
,
所以![]()


![]() .
.
故存在常数![]() ,使得
,使得![]() .
.

【题目】某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:min)绘制了如下茎叶图:
第一种生产方式 | 第二种生产方式 | |||||||||||||||||||
8 | 6 | 5 | 5 | 6 | 8 | 9 | ||||||||||||||
9 | 7 | 6 | 2 | 7 | 0 | 1 | 2 | 2 | 3 | 4 | 5 | 6 | 6 | 8 | ||||||
9 | 8 | 7 | 7 | 6 | 5 | 4 | 3 | 3 | 2 | 8 | 1 | 4 | 4 | 5 | ||||||
2 | 1 | 1 | 0 | 0 | 9 | 0 | ||||||||||||||
(1)根据茎叶图判断哪种生产方式的效率更高?并说明理由;
(2)求40名工人完成生产任务所需时间的中位数m,并将完成生产任务所需时间超过m和不超过m的工人数填入下面的列联表:
超过m | 不超过m | 总计 | |
第一种生产方式 | |||
第二种生产方式 | |||
总计 |
(3)根据(2)中的列表,能否有99%的把握认为两种生产方式的效率有差异?
附: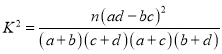 ,
,![]() .
.
【题目】某班随机抽查了![]() 名学生的数学成绩,分数制成如图的茎叶图,其中
名学生的数学成绩,分数制成如图的茎叶图,其中![]() 组学生每天学习数学时间不足
组学生每天学习数学时间不足![]() 个小时,
个小时,![]() 组学生每天学习数学时间达到一个小时,学校规定
组学生每天学习数学时间达到一个小时,学校规定![]() 分及
分及![]() 分以上记为优秀,
分以上记为优秀,![]() 分及
分及![]() 分以上记为达标,
分以上记为达标,![]() 分以下记为未达标.
分以下记为未达标.

(1)根据茎叶图完成下面的列联表:
达标 | 未达标 | 总计 | |
| |||
| |||
总计 |
(2)判断是否有![]() 的把握认为“数学成绩达标与否”与“每天学习数学时间能否达到一小时”有关.
的把握认为“数学成绩达标与否”与“每天学习数学时间能否达到一小时”有关.
参考公式与临界值表: ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|