题目内容
(本题满分16分)
已知函数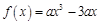 ,
,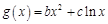 ,且
,且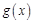 在点
在点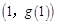 处的切线方程为
处的切线方程为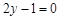 .
.
(1)求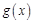 的解析式;
的解析式;
(2)求函数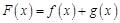 的单调递增区间;
的单调递增区间;
(3)设函数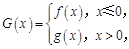 若方程
若方程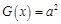 恰四个不同的解,求实数
恰四个不同的解,求实数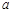 的取值范围.
的取值范围.
已知函数
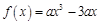 ,
,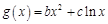 ,且
,且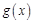 在点
在点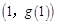 处的切线方程为
处的切线方程为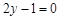 .
.(1)求
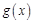 的解析式;
的解析式;(2)求函数
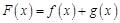 的单调递增区间;
的单调递增区间;(3)设函数
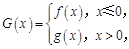 若方程
若方程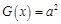 恰四个不同的解,求实数
恰四个不同的解,求实数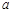 的取值范围.
的取值范围.(1)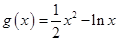 (2)见解析(3)
(2)见解析(3)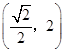
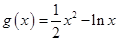 (2)见解析(3)
(2)见解析(3)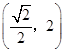
(1)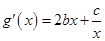 ,由条件,得
,由条件,得
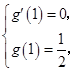 即
即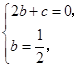 解得
解得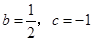 ,所以
,所以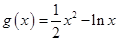 . 3分
. 3分
(2)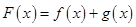
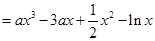 ,其定义域为
,其定义域为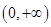 ,
,
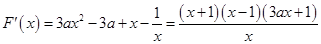 ,
,
令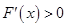 ,得
,得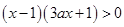 (*) 5分
(*) 5分
①若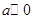 ,则
,则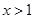 ,即
,即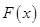 的单调递增区间为
的单调递增区间为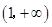 ;
;
②若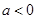 ,(*)式等价于
,(*)式等价于 ,
,
当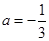 时,
时,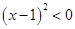 ,无解,即
,无解,即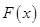 无单调增区间,
无单调增区间,
当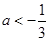 时,则
时,则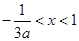 ,即
,即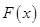 的单调递增区间为
的单调递增区间为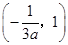 ,
,
当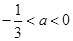 ,则
,则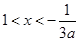 ,即
,即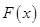 的单调递增区间为
的单调递增区间为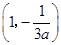 . 8分
. 8分
(3).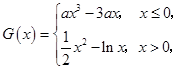 .
.
当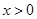 时,
时, ,
,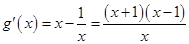 ,
,
令 ,得
,得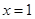 ,且当
,且当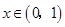 时,
时,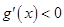 ;当
;当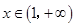 时,
时,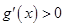 ,
,
所以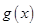 在
在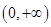 上有极小值,即最小值为
上有极小值,即最小值为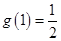 . 10分
. 10分
当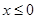 时,
时,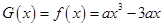 ,
,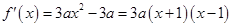 ,
,
令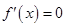 ,得
,得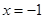 ,
,
①若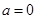 ,方程
,方程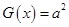 不可能有四个解; 12分
不可能有四个解; 12分
②若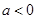 ,当
,当 时,
时,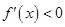 ,当
,当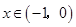 时,
时,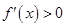 ,
,
所以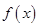 在
在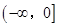 上有极小值且是最小值为
上有极小值且是最小值为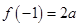 ,
,
又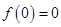 ,
,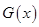 的大致图象如图1所示,
的大致图象如图1所示,
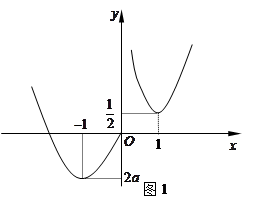
从图象可以看出方程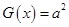 不可能有四个解. 14分
不可能有四个解. 14分
③若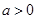 ,当
,当 时,
时,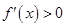 ,当
,当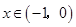 时,
时,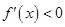 ,
,
所以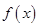 在
在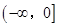 上有极大值且是最大值为
上有极大值且是最大值为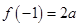 ,
,
又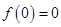 ,
,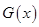 的大致图象如图2所示,
的大致图象如图2所示,
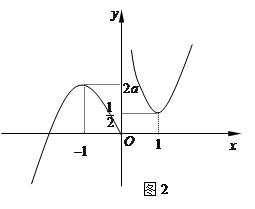
从图象可以看出若方程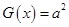 恰四个不同的解,
恰四个不同的解,
必须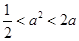 ,解得
,解得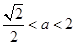 .
.
综上所述,满足条件的实数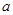 的取值范围是
的取值范围是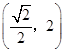 . 16分
. 16分
【命题意图】本题考查导数在函数中应用、函数图像等知识 ,意在考查运算求解能力,数学综合论证能力.
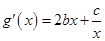 ,由条件,得
,由条件,得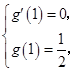 即
即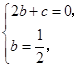 解得
解得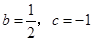 ,所以
,所以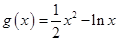 . 3分
. 3分(2)
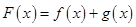
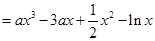 ,其定义域为
,其定义域为 ,
,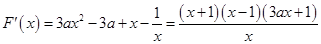 ,
,令
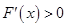 ,得
,得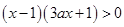 (*) 5分
(*) 5分①若
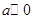 ,则
,则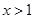 ,即
,即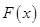 的单调递增区间为
的单调递增区间为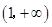 ;
; ②若
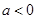 ,(*)式等价于
,(*)式等价于 ,
,当
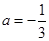 时,
时,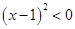 ,无解,即
,无解,即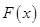 无单调增区间,
无单调增区间,当
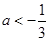 时,则
时,则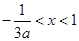 ,即
,即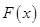 的单调递增区间为
的单调递增区间为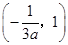 ,
,当
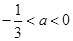 ,则
,则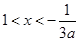 ,即
,即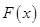 的单调递增区间为
的单调递增区间为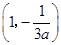 . 8分
. 8分(3).
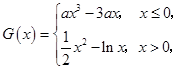 .
.当
 时,
时, ,
,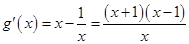 ,
,令
 ,得
,得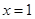 ,且当
,且当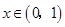 时,
时,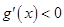 ;当
;当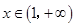 时,
时,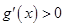 ,
,所以
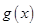 在
在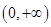 上有极小值,即最小值为
上有极小值,即最小值为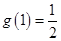 . 10分
. 10分当
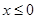 时,
时,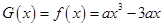 ,
,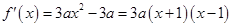 ,
,令
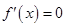 ,得
,得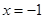 ,
,①若
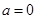 ,方程
,方程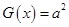 不可能有四个解; 12分
不可能有四个解; 12分②若
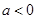 ,当
,当 时,
时,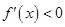 ,当
,当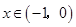 时,
时,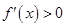 ,
,所以
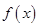 在
在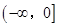 上有极小值且是最小值为
上有极小值且是最小值为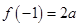 ,
,又
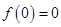 ,
,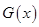 的大致图象如图1所示,
的大致图象如图1所示,
从图象可以看出方程
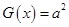 不可能有四个解. 14分
不可能有四个解. 14分③若
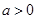 ,当
,当 时,
时,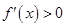 ,当
,当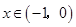 时,
时,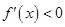 ,
,所以
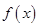 在
在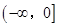 上有极大值且是最大值为
上有极大值且是最大值为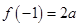 ,
,又
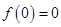 ,
,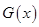 的大致图象如图2所示,
的大致图象如图2所示,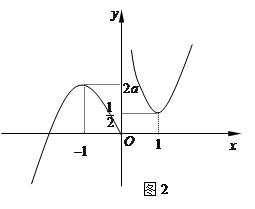
从图象可以看出若方程
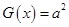 恰四个不同的解,
恰四个不同的解,必须
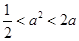 ,解得
,解得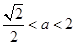 .
.综上所述,满足条件的实数
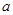 的取值范围是
的取值范围是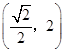 . 16分
. 16分【命题意图】本题考查导数在函数中应用、函数图像等知识 ,意在考查运算求解能力,数学综合论证能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
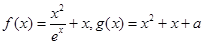 .
.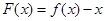 的单调区间和极值;
的单调区间和极值;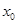 ,使得
,使得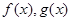 在
在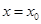 的切线相同?若存在,求出
的切线相同?若存在,求出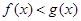 在
在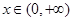 恒成立,求
恒成立,求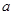 的取值范围.
的取值范围.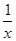 与y2=x3-x2+2x在x=x0处切线的斜率的乘积为3,则x0的值为( )
与y2=x3-x2+2x在x=x0处切线的斜率的乘积为3,则x0的值为( )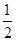
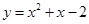 在点
在点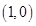 处的切线方程为
处的切线方程为 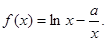
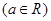
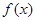 的单调增区间;
的单调增区间;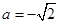 ,求函数
,求函数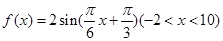 的图像与
的图像与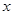 轴交于点
轴交于点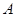 ,过点
,过点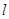 与函数
与函数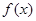 的图像交于
的图像交于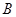
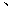
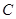 两点,则
两点,则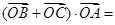 ( )
( )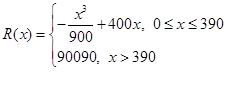 ,则当总利润最大时,每年生产产品的单位数是( )
,则当总利润最大时,每年生产产品的单位数是( )