题目内容
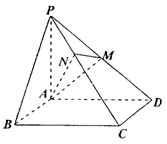
如图,平面α上定点F到定直线l的距离FA=2,曲线C是平面α上到定点F和到定直线l的距离相等的动点P的轨迹.设FB⊥α,且FB=2.
(1)若曲线C上存在点P0,使得P0B⊥AB,试求直线P0B与平面α所成角θ的大小;
(2)对(1)中P0,求点F到平面ABP0的距离h.
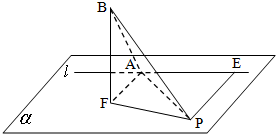
(1)若曲线C上存在点P0,使得P0B⊥AB,试求直线P0B与平面α所成角θ的大小;
(2)对(1)中P0,求点F到平面ABP0的距离h.

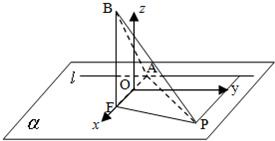
(1)(解法一)如图,以线段FA的中点为原点O,以线段FA所在的直线为x轴,建立空间直角坐标系O-xyz.
由题意,曲线C是平面α上以原点O为顶点,由于在xOy平面内,CF(2,0,0)
是以O为顶点,以x轴为对称轴的抛物线,其方程为y2=4x,
因此,可设P(
,y,0)A(-1,0,0),B(1,0,2),所以,
=(2,0,2),
=(1-
,-y,2).
由P0B⊥AB,得2(1-
)+4=0⇒y=2
,⇒P(3,2
,0)
所以,直线P0B与平面α所成角的大小为arctan
(或arcsin
).
(解法二)如图,以点A为原点O,以线段FA所在的直线为x轴,建立空间直角坐标系O-xyz.
所以,A(0,0,0),B(2,0,2),F(2,0,0),并设P(x,y,0),
由题意,
⇒P(3,2
,0)
所以,直线P0B与平面α所成角的大小为arctan
(或arcsin
).
(2)(解法一)由(1),得△ABP的面积为S△ABP=2
,△AFP的面积为S△AFP=2
,
所以,
×2
h=
×2
×2,
解得,h=
.
(解法二)
=(2,0,2),
=(4,2
,0),设向量
=(x,y,z)
则
所以,平面ABP0的一个法向量
=(3,-2
,-3),∴h=
=
.
由题意,曲线C是平面α上以原点O为顶点,由于在xOy平面内,CF(2,0,0)
是以O为顶点,以x轴为对称轴的抛物线,其方程为y2=4x,
因此,可设P(
| y2 |
| 4 |
| AB |
| PB |
| y2 |
| 4 |
由P0B⊥AB,得2(1-
| y2 |
| 4 |
| 3 |
| 3 |
所以,直线P0B与平面α所成角的大小为arctan
| 1 |
| 2 |
| ||
| 3 |
(解法二)如图,以点A为原点O,以线段FA所在的直线为x轴,建立空间直角坐标系O-xyz.
所以,A(0,0,0),B(2,0,2),F(2,0,0),并设P(x,y,0),
由题意,
|
|
| 3 |
所以,直线P0B与平面α所成角的大小为arctan
| 1 |
| 2 |
| ||
| 3 |
(2)(解法一)由(1),得△ABP的面积为S△ABP=2
| 10 |
| 3 |
所以,
| 1 |
| 3 |
| 10 |
| 1 |
| 3 |
| 3 |
解得,h=
| ||
| 5 |
(解法二)
| AB |
| AP |
| 3 |
| n |
则
|
所以,平面ABP0的一个法向量
| n0 |
| 3 |
|
| ||||
|
|
| ||
| 5 |


练习册系列答案
相关题目