题目内容
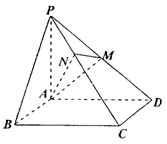
在四棱锥P-ABCD中，ABCD为正方形，PA⊥平面ABCD，若PA=AB，则PC与面PAB所成角的余弦值为______．
∵PA⊥平面ABCD，BC?平面ABCD
∴PA⊥BC，而BC⊥AB，AB∩PA=A
∴BC⊥面PAB
∴∠BPC为PC与面PAB所成角
设PA=PB=BC=1，则PB=
，PC=
∴cos∠BPC=
=
故答案为
∴PA⊥BC，而BC⊥AB，AB∩PA=A
∴BC⊥面PAB
∴∠BPC为PC与面PAB所成角
设PA=PB=BC=1，则PB=
| 2 |
| 3 |
∴cos∠BPC=
| ||
|
| ||
| 3 |
故答案为
| ||
| 3 |
练习册系列答案
心算口算巧算一课一练系列答案
相关题目
