题目内容
在长为100千米的铁路线AB旁的C处有一个工厂,工厂与铁路的距离CA为20千米.由铁路上的B处向工厂提供原料,公路与铁路每吨千米的货物运价比为5∶3,为节约运费,在铁路的D处修一货物转运站,设AD距离为x千米,沿CD直线修一条公路(如图).
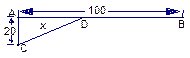
(1)将每吨货物运费y(元)表示成x的函数.
(2)当x为何值时运费最省?
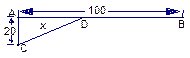
(1)将每吨货物运费y(元)表示成x的函数.
(2)当x为何值时运费最省?
x为15千米时运费最省
(1)设公路与铁路每吨千米的货物运价分别为5k、3k(元)(k为常数)AD=x,则DB=100-x.

∴每吨货物运费y=(100-x)·3k+ ·5k(元)
·5k(元)
(2)令y′=-3k+5k· ·k=0
·k=0
∴5x-3 =0
=0
∵x>0,∴解得x=15
当0<x<15时,y′<0;当x>15时,y′>0
∴当x=15时,y有最小值.
答:当x为15千米时运费最省 .

∴每吨货物运费y=(100-x)·3k+
 ·5k(元)
·5k(元)(2)令y′=-3k+5k·
 ·k=0
·k=0∴5x-3
 =0
=0∵x>0,∴解得x=15
当0<x<15时,y′<0;当x>15时,y′>0
∴当x=15时,y有最小值.
答:当x为15千米时运费最省 .

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
 为曲线
为曲线 在点(1,0)处的切线,直线
在点(1,0)处的切线,直线 为该曲线的另一条切线,且
为该曲线的另一条切线,且

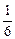 处的切线的倾斜角是
处的切线的倾斜角是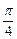
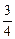 π
π x2-2x在点(1,-
x2-2x在点(1,-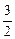 )处的切线的倾斜角为__________.
)处的切线的倾斜角为__________.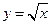 上有点
上有点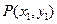 ,与曲线切于点
,与曲线切于点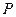 的切线为
的切线为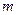 ,若直线
,若直线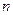 过
过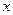 轴于点
轴于点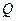 ,又作
,又作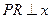 轴于
轴于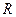 ,求
,求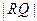 的长。
的长。 是函数
是函数 的反函数,且
的反函数,且 ,则
,则



