题目内容
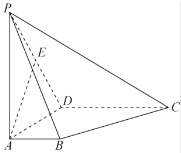
【题目】如图在四棱锥![]() 中,侧棱
中,侧棱![]() 平面
平面![]() ,底面
,底面![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为侧棱
为侧棱![]() 中点.
中点.
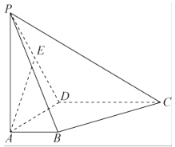
(1)设![]() 为棱
为棱![]() 上的动点,试确定点
上的动点,试确定点![]() 的位置,使得平面
的位置,使得平面![]() 平面
平面![]() ,并写出证明过程;
,并写出证明过程;
(2)求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)当![]() 为
为![]() 中点时,满足平面
中点时,满足平面![]() 平面
平面![]() ;证明见解析(2)
;证明见解析(2)![]()
【解析】
(1)当![]() 为
为![]() 中点时,通过证明
中点时,通过证明![]() ,
,![]() 得证平面
得证平面![]() 平面
平面![]() ;
;
(2)由等体积法可得![]() ,即可求得点到平面距离.
,即可求得点到平面距离.
(1)当![]() 为
为![]() 中点时,满足平面
中点时,满足平面![]() 平面
平面![]() ,
,

证明如下:
在梯形![]() 中,因为
中,因为![]() ,
,![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,
,
即四边形![]() 为平行四边形,所以
为平行四边形,所以![]() ,即
,即![]() 平面
平面![]() ,
,
在![]() 中,因为
中,因为![]() 、
、![]() 分别为
分别为![]() 、
、![]() 中点,所以
中点,所以![]() ,即
,即![]() 平面
平面![]() .
.
又因为![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() .
.
(2)因为![]() 平面
平面![]() ,所以
,所以![]() ,
,
因为![]() ,所以
,所以![]()
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() .
.
所以![]() 平面
平面![]() ,所以
,所以![]()
所以![]() 为直角三角形.
为直角三角形.
因为![]() ,所以
,所以![]() ,
,![]()
在梯形![]() 中,
中,![]() .
.
由等体积法可得![]() ,所以
,所以![]() ,解得
,解得![]() .
.
所以点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
【题目】现从某医院中随机抽取了![]() 位医护人员的关爱患者考核分数(患者考核:
位医护人员的关爱患者考核分数(患者考核:![]() 分制),用相关的特征量
分制),用相关的特征量![]() 表示;医护专业知识考核分数(试卷考试:
表示;医护专业知识考核分数(试卷考试:![]() 分制),用相关的特征量
分制),用相关的特征量![]() 表示,数据如下表:
表示,数据如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)求![]() 关于
关于![]() 的线性回归方程(计算结果精确到
的线性回归方程(计算结果精确到![]() );
);
(2)利用(1)中的线性回归方程,分析医护专业考核分数的变化对关爱患者考核分数的影响,并估计当某医护人员的医护专业知识考核分数为![]() 分时,他的关爱患者考核分数(精确到
分时,他的关爱患者考核分数(精确到![]() ).
).
参考公式及数据:回归直线方程![]() 中斜率和截距的最小二乘法估计公式分别为
中斜率和截距的最小二乘法估计公式分别为
 ,其中
,其中![]() .
.