题目内容
【题目】已知长度为![]() 的线段
的线段![]() 的两个端点
的两个端点![]() 分别在
分别在![]() 轴和
轴和![]() 轴上运动,动点
轴上运动,动点![]() 满足
满足![]() ,设动点
,设动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() ,且斜率不为零的直线
,且斜率不为零的直线![]() 与曲线
与曲线![]() 交于两点
交于两点![]() ,在
,在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得直线
,使得直线![]() 与
与![]() 的斜率之积为常数?若存在,求出定点
的斜率之积为常数?若存在,求出定点![]() 的坐标以及此常数;若不存在,请说明理由.
的坐标以及此常数;若不存在,请说明理由.
【答案】(1)![]() (2)存在两个定点
(2)存在两个定点![]() ,
,![]() ,使得直线
,使得直线![]() 与
与![]() 的斜率之积为常数,当定点为
的斜率之积为常数,当定点为![]() 时,常数为
时,常数为![]() ,当定点为
,当定点为![]() 时,常数为
时,常数为![]()
【解析】
(1)设![]() ,
,![]() ,
,![]() ,利用向量关系
,利用向量关系![]() 坐标化,可得曲线
坐标化,可得曲线![]() 的方程;
的方程;
(2)由题意设直线![]() 的方程为
的方程为![]() ,
,![]() ,
,![]() ,假设存在定点
,假设存在定点![]() ,使得直线
,使得直线![]() 与
与![]() 的斜率之积为常数,将
的斜率之积为常数,将![]() 表示成关于
表示成关于![]() 的函数,利用恒成立问题,可得定点坐标.
的函数,利用恒成立问题,可得定点坐标.
(1)设![]() ,
,![]() ,
,![]() ,
,
由于![]() ,所以
,所以![]() ,
,
即![]() ,所以
,所以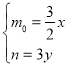 .又因为
.又因为![]() ,所以
,所以![]() ,
,
从而![]() ,即曲线
,即曲线![]() 的方程为
的方程为![]() .
.
(2)由题意设直线![]() 的方程为
的方程为![]() ,
,![]() ,
,![]() ,
,
由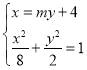 得
得![]() ,所以
,所以 ,
,
故![]() ,
,![]() .
.
假设存在定点![]() ,使得直线
,使得直线![]() 与
与![]() 的斜率之积为常数,则
的斜率之积为常数,则
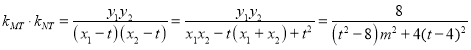 .
.
当![]() ,且
,且![]() 时,
时,![]() 为常数,解得
为常数,解得![]() .
.
显然当![]() 时,常数为
时,常数为![]() ;当
;当![]() 时,常数为
时,常数为![]() .
.
所以存在两个定点![]() ,
,![]() ,使得直线
,使得直线![]() 与
与![]() 的斜率之积为常数,当定点为
的斜率之积为常数,当定点为![]() 时,常数为
时,常数为![]() ,当定点为
,当定点为![]() 时,常数为
时,常数为![]() .
.

 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案【题目】为了使房价回归到收入可支撑的水平,让全体人民住有所居,近年来全国各一、二线城市打击投机购房,陆续出台了住房限购令.某市一小区为了进一步了解已购房民众对市政府岀台楼市限购令的认同情况,随机抽取了本小区50户住户进行调查,各户人平均月收入(单位:千元)的户数频率分布直方图如图,其中赞成限购的户数如下表:
人平均月收入 |
|
|
|
|
|
|
赞成户数 | 4 | 9 | 12 | 6 | 3 | 1 |
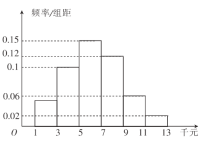
(1)若从人平均月收入在![]() 的住户中再随机抽取两户,求所抽取的两户至少有一户赞成楼市限购令的概率;
的住户中再随机抽取两户,求所抽取的两户至少有一户赞成楼市限购令的概率;
(2)若将小区人平均月收入不低于7千元的住户称为“高收入户”,人平均月收入低于7千元的住户称为“非高收入户”根据已知条件完成如图所给的![]() 列联表,并说明能否有
列联表,并说明能否有![]() 的把握认为“收入的高低”与“赞成楼市限购令”有关.
的把握认为“收入的高低”与“赞成楼市限购令”有关.
非高收入户 | 高收入户 | ||
赞成 | |||
不赞成 | |||
总计 |
附:临界值表
| 0.1 | 0.05 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.63.5 | 10.828 |
参考公式: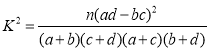 ,
,![]() .
.