题目内容
8.已知一圆的圆心为(2,3),一条直径的端点分别在x,y轴上,则此圆的方程是(x-2)2+(y-3)2=13.分析 直径的两个端点分别A(a,0)B(0,b),圆心(2,3)为AB的中点,利用中点坐标公式求出a,b后,再利用两点距离公式求出半径.
解答 解:设直径的两个端点分别A(a,0)B(0,b).
圆心为点(2,3),由中点坐标公式得,a=4,b=6,∴r=$\frac{1}{2}AB$=$\sqrt{13}$,
则此圆的方程是(x-2)2+(y-3)2=13,
故答案为:(x-2)2+(y-3)2=13.
点评 本题考查圆的方程求解,确定圆心、半径即能求出圆的标准方程.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.已知过点(-2,3)可以作圆(x-a)2+(y-2)2=9的两条切线,则a的范围是( )
| A. | (-∞,-3)∪(3,+∞) | B. | $(-∞,-2-2\sqrt{2})∪(-2+2\sqrt{2},+∞)$ | ||
| C. | (-3,3) | D. | $(-2-2\sqrt{2},-2+2\sqrt{2})$ |
18.在直角坐标系xOy中,点M的坐标是(1,-$\sqrt{3}$),若以原点O为极点,x轴的非负半轴为极轴建立极坐标系,则点M的极坐标可以为( )
| A. | (2,$\frac{π}{3}$) | B. | (2,$\frac{2π}{3}$) | C. | (2,-$\frac{π}{3}$) | D. | (2,2kπ+$\frac{π}{3}$)(k∈Z) |
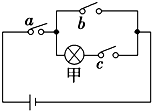 如图所示的电路有a,b,c三个开关,每个开关开或关的概率都是$\frac{1}{2}$,且是相互独立的,则灯泡甲亮的概率为$\frac{1}{8}$.
如图所示的电路有a,b,c三个开关,每个开关开或关的概率都是$\frac{1}{2}$,且是相互独立的,则灯泡甲亮的概率为$\frac{1}{8}$. 如图,在等腰梯形ABCD中,AB∥CD,延长AB到点E,使∠BEC=∠CAD.若AC=$\sqrt{2}$,CD=CE=1,则BC=$\frac{\sqrt{2}}{2}$.
如图,在等腰梯形ABCD中,AB∥CD,延长AB到点E,使∠BEC=∠CAD.若AC=$\sqrt{2}$,CD=CE=1,则BC=$\frac{\sqrt{2}}{2}$.