题目内容
9.等比数列{an}的前n项和为Sn,且an+1=2Sn+$\frac{1}{2}$(n∈N*)(1)求数列{an}的通项公式;
(2)在an和an+1之间插入n个实数,使得这n+2个数依次组成公差为dn的等差数列,设数列{$\frac{1}{{d}_{n}}$}的前n项和为Tn,求证:$\frac{38}{12}$≤Tn<$\frac{15}{4}$.
分析 (I)由an+1=2Sn+$\frac{1}{2}$(n∈N*),可得an=2sn-1+$\frac{1}{2}$(n≥2),两式相减可得an+1=3an(n≥2),结合已知等比数列的条件可得a2=3a1,可求a1,从而可求通项.
(II)等差数列的性质可知dn=$\frac{{a}_{n+1}-{a}_{n}}{n+1}$=$\frac{{3}^{n-1}}{n+1}$,利用错位相减可求数列的和,利用放缩法即可得出结论.
解答 解:(I)由an+1=2Sn+$\frac{1}{2}$(n∈N*),
可得an=2sn-1+$\frac{1}{2}$(n≥2)
两式相减可得,an+1-an=2an
即an+1=3an(n≥2)
又∵a2=2a1+$\frac{1}{2}$,且数列{an}为等比数列
∴a2=3a1
则2a1+$\frac{1}{2}$=3a1
∴a1=$\frac{1}{2}$
∴${a}_{n}=\frac{1}{2}•{3}^{n-1}$.
(II)由(I)知,${a}_{n}=\frac{1}{2}•{3}^{n-1}$.,an+1=$\frac{1}{2}$•3n
∵an+1=an+(n+1)dn
∴dn=$\frac{{a}_{n+1}-{a}_{n}}{n+1}$=$\frac{{3}^{n-1}}{n+1}$,
∴Tn=$\frac{2}{{3}^{0}}$+$\frac{3}{{3}^{1}}$+$\frac{4}{{3}^{2}}$+…+$\frac{n}{{3}^{n-2}}$+$\frac{n+1}{{3}^{n-1}}$,
$\frac{1}{3}$Tn=$\frac{2}{{3}^{1}}$+$\frac{3}{{3}^{2}}$+$\frac{4}{{3}^{3}}$+…+$\frac{n}{{3}^{n-1}}$+$\frac{n+1}{{3}^{n}}$,
两式相减可得,$\frac{2}{3}{T}_{n}$=2+$\frac{1}{3}$+$\frac{1}{{3}^{2}}$+…+$\frac{1}{{3}^{n-1}}$-$\frac{n+1}{{3}^{n}}$=2+$\frac{\frac{1}{3}[1-(\frac{1}{3})^{n-1}]}{1-\frac{1}{3}}$-$\frac{n+1}{{3}^{n}}$=$\frac{5}{2}$-$\frac{1}{2}•(\frac{1}{3})^{n-1}$-(n+1)•$(\frac{1}{3})^{n}$,
∴Tn=$\frac{15}{4}$-$\frac{1}{4}•(\frac{1}{3})^{n-2}$-$\frac{1}{2}(n+1)•(\frac{1}{3})^{n-1}$<$\frac{15}{4}$,
又∵Tn+1-Tn=(n+2)•$(\frac{1}{3})^{n}$>0,∴Tn≥T1=2,
∴2≤Tn<$\frac{15}{4}$.
点评 本题主要考查了等比数列的通项公式的应用及由数列的递推公式求解通项,数列求和的错位相减求和方法的应用是解答本题的关键,属于中档题.

| A. | 充分接近1的数 | B. | 大于0小于20的整数 | ||
| C. | 所有有理数 | D. | 数轴上到原点的距离等于1的点 |
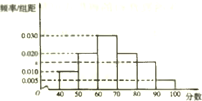 某校随机抽取20名学生在一次知识竞赛中的成绩(均为整数),并绘制频率分布直方图(如图所示),其中样本数据分组区间为:[40,50)、[50,60)、[60,70)、[70,80)、[80,90),[90,100].
某校随机抽取20名学生在一次知识竞赛中的成绩(均为整数),并绘制频率分布直方图(如图所示),其中样本数据分组区间为:[40,50)、[50,60)、[60,70)、[70,80)、[80,90),[90,100].