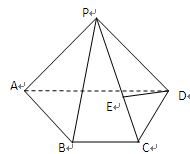
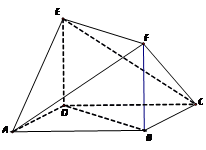
题目内容
已知斜三棱柱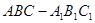 的各棱长均为2, 侧棱
的各棱长均为2, 侧棱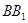 与底面
与底面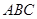 所成角为
所成角为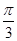 ,且侧面
,且侧面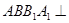 底面
底面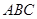 .
.
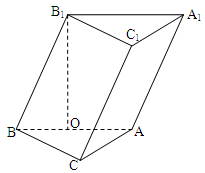
 (1)证明:点
(1)证明:点 在平面
在平面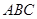 上的射影
上的射影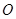 为
为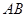 的中点;
的中点;



 (2)求二面角
(2)求二面角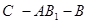 的大小;
的大小;
(3)求点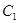 到平面
到平面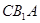 的距离.
的距离.
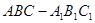 的各棱长均为2, 侧棱
的各棱长均为2, 侧棱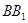 与底面
与底面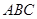 所成角为
所成角为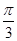 ,且侧面
,且侧面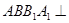 底面
底面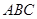 .
.
 (1)证明:点
(1)证明:点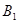 在平面
在平面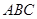 上的射影
上的射影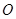 为
为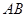 的中点;
的中点;


 (2)求二面角
(2)求二面角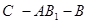 的大小;
的大小;(3)求点
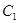 到平面
到平面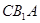 的距离.
的距离.(1)见解析 (2)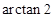 (3)
(3)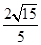
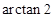 (3)
(3)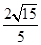
【错解分析】对于立体几何的角和距离,一定要很好的理解“作,证,”三个字
【正解】解:(1)证明:过B1点作B1O⊥BA。∵侧面ABB1A1⊥底面ABC
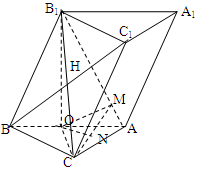
∴A1O⊥面ABC ∴∠B1BA是侧面BB1与底面ABC倾斜角∴∠B1BO=
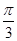
在Rt△B1OB中,BB1=2,∴BO=
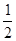 BB1=1
BB1=1又∵BB1=AB,∴BO=
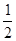 AB ∴O是AB的中点,
AB ∴O是AB的中点,即点B1在平面ABC上的射影O为AB的中点.
(2)连接AB1过点O作OM⊥AB1,连线CM,OC,
∵OC⊥AB,平面ABC⊥平面AA1BB1∴OC⊥平面AABB.∴OM是斜线CM在平面AA1B1B的射影 ∵OM⊥AB1∴AB1⊥CM ∴∠OMC是二面角C—AB1—B的平面角
在Rt△OCM中,OC=
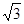 ,OM=
,OM=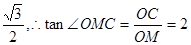
∴∠OMC=
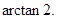 ∴二面角C—AB1—B的大小为
∴二面角C—AB1—B的大小为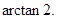
(3)过点O作ON⊥CM,∵AB1⊥平面OCM,∴AB1⊥ON
∴ON⊥平面AB1C。∴ON是O点到平面AB1C的距离
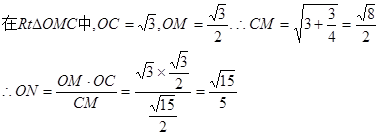
连接BC1与B1C相交于点H,则H是BC1的中点,∴B与C1到平面ACB1的相导。
又∵O是AB的中点 ∴B到平面AB1C的距离是O到平面AB1C距离的2倍
∴点
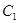 到平面AB1C距离为
到平面AB1C距离为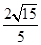 .
.
练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
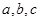 是三条不同的直线,
是三条不同的直线,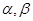 是两个不同的平面,在下列命题:
是两个不同的平面,在下列命题: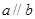 ,且
,且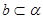 ,则
,则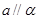
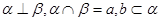 ,且
,且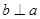 ,则
,则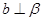
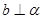 ,则
,则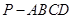 ,面
,面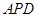 ⊥面
⊥面 .侧面
.侧面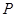 为直角顶点的等腰直角三角形,底面
为直角顶点的等腰直角三角形,底面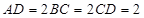 ,
,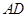 ∥
∥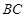 ,
,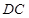 ⊥
⊥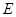 为
为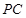 上一点,且
上一点,且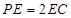 .
.
 ⊥
⊥ ;
;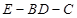 的正弦值.
的正弦值.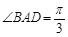 .
.
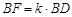 ,当二面角
,当二面角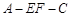 为直二面角时,求k的值.
为直二面角时,求k的值.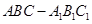 中,底面是正三角形,侧棱
中,底面是正三角形,侧棱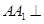 底面
底面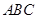 ,点
,点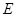 是侧面
是侧面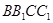 的中心,若
的中心,若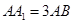 ,则直线
,则直线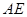 与平面
与平面
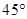


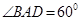 且边长是2的菱形
且边长是2的菱形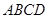 ,沿它的对角线
,沿它的对角线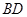 折成60°的二面角,则( )
折成60°的二面角,则( )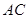 与
与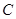 到平面
到平面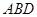 的距离是 .
的距离是 .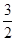
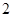
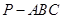 中,
中,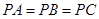 ,
,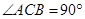 ,
,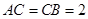 .
. 
 平面
平面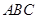 ;
;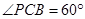 时,求三棱锥
时,求三棱锥 的体积.
的体积.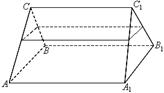
 ⊥平面
⊥平面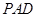 ,
,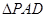 是直角三角形,
是直角三角形,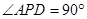 ,四边形
,四边形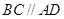 ,
,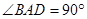 ,
,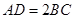 ,且
,且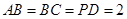 ,
,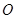 是
是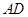 的中点,
的中点,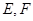 分别是
分别是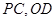 的中点.
的中点. 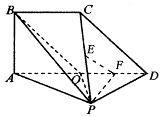
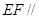 平面
平面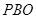 ;
;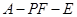 的正切值.
的正切值.