题目内容
(本小题满分12分)
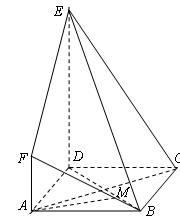
如图,菱形ABCD与矩形BDEF所在平面互相垂直,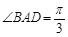 .
.
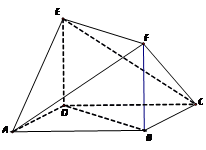
(1)求证:FC∥平面AED;
(2)若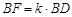 ,当二面角
,当二面角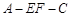 为直二面角时,求k的值.
为直二面角时,求k的值.
如图,菱形ABCD与矩形BDEF所在平面互相垂直,
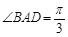 .
.
(1)求证:FC∥平面AED;
(2)若
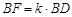 ,当二面角
,当二面角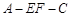 为直二面角时,求k的值.
为直二面角时,求k的值.(1)根据面面平行的性质定理来分析得到证明,关键是证明平面FBC∥平面EDA
(2)
(2)

试题分析:(1)证明:
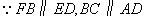 ,
,平面FBC∥平面EDA

故
 平面
平面
(2)取EF,BD的中点M,N. 由于AE=AF=CE=CF
所以
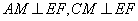 ,且
,且 。
。∴
 就是二面角
就是二面角 的平面角
的平面角连接AC,当
 =90°即二面角
=90°即二面角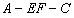 为直二面角时,
为直二面角时,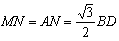 ,
,即

点评:解决立体几何中的平行和垂直的证明,需要熟练的运用线面平行和垂直 判定定理和性质定理阿丽解答。而对于角的求解,通常就是利用定义作出角,然后结合三角形来得到结论,属于中档题。

练习册系列答案
相关题目
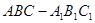 的各棱长均为2, 侧棱
的各棱长均为2, 侧棱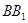 与底面
与底面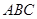 所成角为
所成角为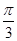 ,且侧面
,且侧面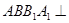 底面
底面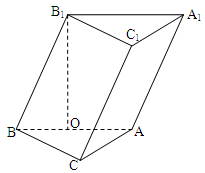
 (1)证明:点
(1)证明:点 在平面
在平面 为
为 的中点;
的中点;
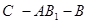 的大小;
的大小;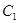 到平面
到平面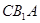 的距离.
的距离. 中,
中,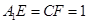 .
.
 与
与 所成角的余弦值;
所成角的余弦值; 与平面
与平面 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.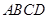 中,
中,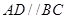 ,
,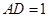 ,
,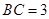 ,
,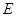 为
为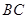 上一点,
上一点, 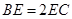 ,且
,且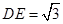 .将梯形
.将梯形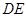 折成直二面角
折成直二面角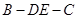 ,如图2所示.
,如图2所示.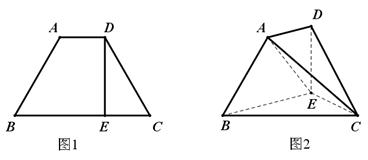
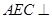 平面
平面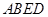 ;
; 关于点
关于点 的对称点为
的对称点为 ,点
,点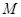 在
在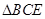 所在平面内,且直线
所在平面内,且直线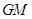 与平面
与平面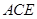 所成的角为
所成的角为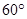 ,试求出点
,试求出点 的最短距离.
的最短距离. β=m,n与α、β所成的角相等,则m⊥n
β=m,n与α、β所成的角相等,则m⊥n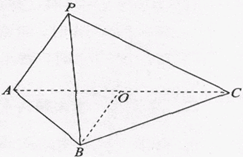
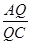 的值;若不存在,说明理由。
的值;若不存在,说明理由。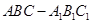 中,侧棱
中,侧棱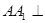 底面
底面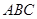 ,
,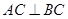 ,
,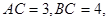
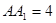 ,
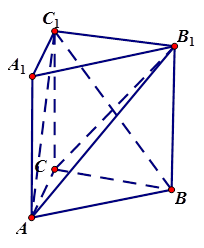
,
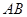 与
与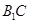 所成角的余弦值;
所成角的余弦值;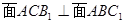
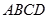 是边长为
是边长为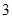 的正方形,
的正方形,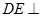 平面
平面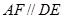 ,
,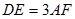 ,
,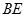 与平面
与平面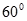 .
.
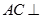 平面
平面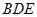 ;
;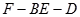 的余弦值;
的余弦值;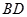 上是否存在点
上是否存在点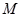 ,使得
,使得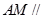 平面
平面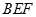 ?若存在,试确定点
?若存在,试确定点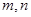 是两条不同的直线,
是两条不同的直线,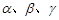 是三个不同的平面.给出下列四个命题:
是三个不同的平面.给出下列四个命题: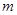 ⊥
⊥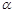 ,
, 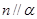 ,则
,则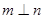 ;
;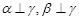 ,则
,则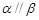 ;
;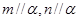 ,则
,则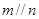 ;
;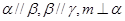 ,则
,则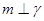 .
.