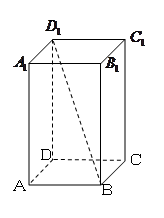题目内容
(本小题满分12分)
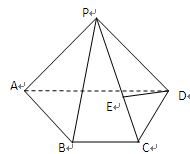
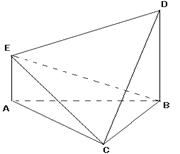
四棱锥 ,面
,面 ⊥面
⊥面 .侧面
.侧面 是以
是以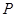 为直角顶点的等腰直角三角形,底面
为直角顶点的等腰直角三角形,底面 为直角梯形,
为直角梯形,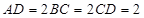 ,
,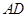 ∥
∥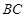 ,
,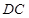 ⊥
⊥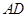 ,
,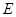 为
为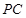 上一点,且
上一点,且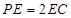 .
.
(Ⅰ)求证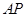 ⊥
⊥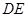 ;
;
(Ⅱ)求二面角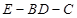 的正弦值.
的正弦值.
四棱锥
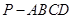 ,面
,面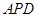 ⊥面
⊥面 .侧面
.侧面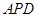 是以
是以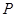 为直角顶点的等腰直角三角形,底面
为直角顶点的等腰直角三角形,底面 为直角梯形,
为直角梯形,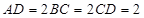 ,
,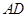 ∥
∥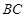 ,
,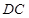 ⊥
⊥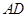 ,
,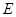 为
为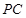 上一点,且
上一点,且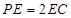 .
.
(Ⅰ)求证
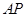 ⊥
⊥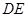 ;
;(Ⅱ)求二面角
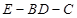 的正弦值.
的正弦值.(Ⅰ)先证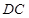 ⊥面
⊥面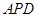 ,再证
,再证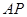 ⊥面
⊥面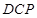 ,进而得证;
,进而得证;
(Ⅱ)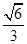
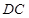 ⊥面
⊥面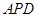 ,再证
,再证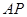 ⊥面
⊥面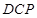 ,进而得证;
,进而得证;(Ⅱ)
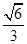
试题分析:(Ⅰ)面
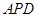 ⊥面
⊥面 且交线为
且交线为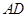 又
又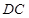 ⊥
⊥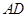 ,
,∴
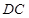 ⊥面
⊥面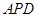 ,
,∴
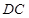 ⊥
⊥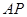 , ……3分
, ……3分∵
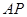 ⊥
⊥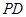 ,
,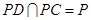 ,
,∴
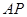 ⊥面
⊥面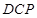 ,
,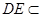
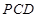 , ……5分
, ……5分∴
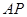 ⊥
⊥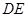 . ……6分
. ……6分(Ⅱ)设
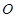 为
为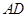 中点,则
中点,则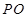 ⊥
⊥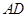 ,∴
,∴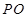 ⊥面
⊥面 ,
,建系如图,则
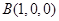
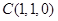
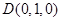
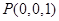
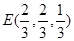 ,
,∴
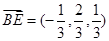 ,
,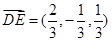 , ……8分
, ……8分设
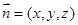 为面
为面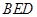 的法向量,
的法向量,则
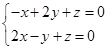 ,∴
,∴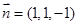 为面
为面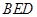 的一个法向量, ……9分
的一个法向量, ……9分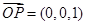 为面
为面 的法向量, ……10分
的法向量, ……10分∴
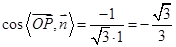 , ……11分
, ……11分∴二面角
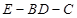 的正弦值为
的正弦值为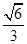 . ……12分
. ……12分点评:用定理证明立体几何问题时要紧扣定理,定理中要求的条件一个也不能漏;用空间向量求解二面角时,要仔细计算,还要注意题目中的二面角时锐角还是钝角.

练习册系列答案
相关题目
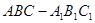 的各棱长均为2, 侧棱
的各棱长均为2, 侧棱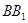 与底面
与底面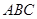 所成角为
所成角为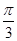 ,且侧面
,且侧面 底面
底面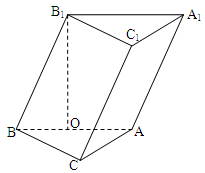
 (1)证明:点
(1)证明:点 在平面
在平面 为
为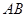 的中点;
的中点;
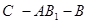 的大小;
的大小;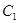 到平面
到平面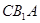 的距离.
的距离.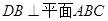 ,
,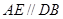 ,
,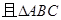 是边长为2的等边三角形,
是边长为2的等边三角形,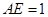 ,CD与平面ABDE所成角的正弦值为
,CD与平面ABDE所成角的正弦值为 .
.
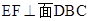 ,若存在,求线段DF的长度,若不存在,说明理由;
,若存在,求线段DF的长度,若不存在,说明理由;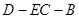 的平面角的余弦值.
的平面角的余弦值.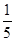 B.
B. 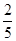 C.
C. 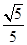 D.
D. 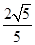
 中,
中,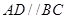 ,
,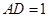 ,
,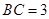 ,
,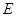 为
为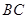 上一点,
上一点, 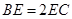 ,且
,且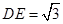 .将梯形
.将梯形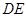 折成直二面角
折成直二面角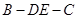 ,如图2所示.
,如图2所示.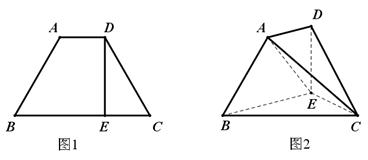
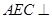 平面
平面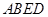 ;
;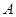 关于点
关于点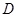 的对称点为
的对称点为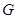 ,点
,点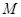 在
在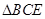 所在平面内,且直线
所在平面内,且直线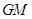 与平面
与平面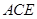 所成的角为
所成的角为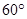 ,试求出点
,试求出点 的最短距离.
的最短距离. α,n
α,n β=m,n与α、β所成的角相等,则m⊥n
β=m,n与α、β所成的角相等,则m⊥n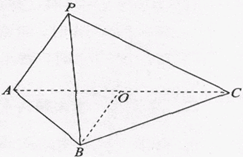
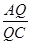 的值;若不存在,说明理由。
的值;若不存在,说明理由。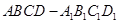 的底面是边长为1的正方形,侧棱长
的底面是边长为1的正方形,侧棱长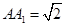 ,则异面直线
,则异面直线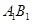 与
与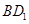 的夹角大小等于___________.
的夹角大小等于___________.