题目内容
数列 的前
的前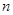 项的和为
项的和为
 的前
的前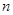 项的和为
项的和为A. | B. |
C. | D. |
C
试题分析:
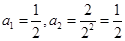 。故
。故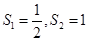 。当
。当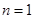 时,
时,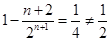 ,排除A;
,排除A;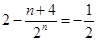 ,排除D。当
,排除D。当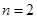 时,
时, ,排除B。选C。
,排除B。选C。点评:错位相减法是求“差比积”数列前n项和的基本方法,是高考考查重点之一。对选择题,则不拘泥于常规,利用“特值法”反映解题的灵活性。

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
题目内容
 的前
的前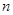 项的和为
项的和为A. | B. |
C. | D. |
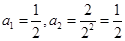 。故
。故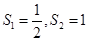 。当
。当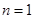 时,
时,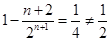 ,排除A;
,排除A;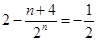 ,排除D。当
,排除D。当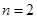 时,
时, ,排除B。选C。
,排除B。选C。
 小学课时特训系列答案
小学课时特训系列答案