题目内容
(本小题满分14分)已知一个数列 的各项都是1或2.首项为1,且在第
的各项都是1或2.首项为1,且在第 个1和第
个1和第 个1之间有
个1之间有 个2,即1,2,1,2,2,2,1,2,2,2,2,2,1,….记数列的前
个2,即1,2,1,2,2,2,1,2,2,2,2,2,1,….记数列的前 项的和为
项的和为 .参考:31×32=992,32×33=1056,44×45=1980,45×46=2070
.参考:31×32=992,32×33=1056,44×45=1980,45×46=2070
(I)试问第10个1为该数列的第几项?
(II)求 和
和 ;
;
(III)是否存在正整数 ,使得
,使得 ?如果存在,求出
?如果存在,求出 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
 的各项都是1或2.首项为1,且在第
的各项都是1或2.首项为1,且在第 个1和第
个1和第 个1之间有
个1之间有 个2,即1,2,1,2,2,2,1,2,2,2,2,2,1,….记数列的前
个2,即1,2,1,2,2,2,1,2,2,2,2,2,1,….记数列的前 项的和为
项的和为 .参考:31×32=992,32×33=1056,44×45=1980,45×46=2070
.参考:31×32=992,32×33=1056,44×45=1980,45×46=2070(I)试问第10个1为该数列的第几项?
(II)求
 和
和 ;
;(III)是否存在正整数
 ,使得
,使得 ?如果存在,求出
?如果存在,求出 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.(I)91(项);(II) ;
;
(III)存在 =993+29=1022,使
=993+29=1022,使 .
.
 ;
;(III)存在
 =993+29=1022,使
=993+29=1022,使 .
.试题分析:(1)根据题意将第
 个1与第
个1与第 个1前的2记为第
个1前的2记为第 对,那么结合已知条件得到前
对,那么结合已知条件得到前 对共有项数为
对共有项数为
(2)因44×45=1980,45×46=2070,2012-1980=32,
故第2012项在第45对中的第32个数。
(3)由于前k对所在全部项的和为
 ,可知结论。
,可知结论。解:将第
 个1与第
个1与第 个1前的2记为第
个1前的2记为第 对,
对,即
 为第1对,共
为第1对,共 项;
项; 为第2对,共
为第2对,共 项;……;
项;……; 为第
为第 对,共
对,共 项;
项;故前
 对共有项数为
对共有项数为 .
. (I)第10个1所在的项之前共有9对,所以10个1为该数列的
9×(9+1)+1=91(项) …………3分
(II)因44×45=1980,45×46=2070,2012-1980=32,
故第2012项在第45对中的第32个数,从而

又前2012项中共有45个1,其余2012-45=1967个数均为2,
于是
 ……………………7分
……………………7分(III)前k对所在全部项的和为
 ,易得,
,易得, ,
, ,
,即
 且自第994项到第1056项均为2,而2012-1954=58能被2整除,
且自第994项到第1056项均为2,而2012-1954=58能被2整除,故存在
 =993+29=1022,使
=993+29=1022,使 . ……………………14分
. ……………………14分点评:解决该试题的关键是先将数列分组,便于发现规律,如分为(1,2),(1,2,2,2),(1,2,2,2,2,2)…,每组的项数构成数列2,4,6,…,发现将第
 个1与第
个1与第 个1前的2记为第
个1前的2记为第 对,则前
对,则前 对共有项数为
对共有项数为 最后数列分组求和即可。
最后数列分组求和即可。
练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
 }中,若
}中,若 ,则
,则 ( )
( )
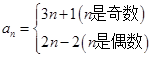 ,则
,则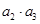 等于( )
等于( ) 的前
的前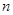 项的和为
项的和为



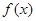 定义如下表,数列
定义如下表,数列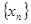 满足
满足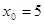 ,且对任意的自然数均有
,且对任意的自然数均有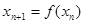 ,则
,则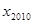 等于( )
等于( )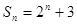 ,则
,则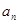 =_________.
=_________.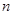 项和为
项和为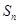 ,满足an+1=an–an–1(n≥2),
,满足an+1=an–an–1(n≥2),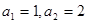 ,则
,则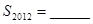
 的所有项按照从大到小,左大右小的原则写成如图所示的数表,第
的所有项按照从大到小,左大右小的原则写成如图所示的数表,第 行有
行有 个数,第
个数,第 个数(从左数起)记为
个数(从左数起)记为 ,则
,则 可记为_________.
可记为_________.
 ,则a5= .
,则a5= .